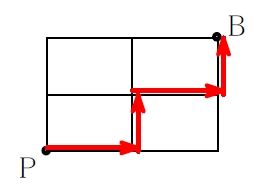
「田」 の端から端まで \(6\) 通り!
準備として, 「順列・組合せ」 について理解しておきましょう.
■最短経路数 って?■
主に格子状の図形の線上を通り, 図形上の \(2\) 点を遠回りせずに結ぶ場合の数.
■積の法則■
家から学校までの通学路が何通りあるかを求めよう.
まずは途中に病院があって,
家から病院までの道が \(\color{royalblue}{2}\) 通り, 病院から学校までの道が \(\color{magenta}{3}\) 通り
ある場合, 通学路の総数は
\(\color{royalblue}{2}\times\color{magenta}{3}=6\ [通り]\)
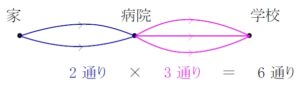
このように,
\(\color{red}{1}\) つの分岐点を通過するとき, 前後の経路数をかけ算
すればよい.
■和の法則■
次に, 家から学校までの道に病院と薬局がありどちらかの経由でしかいけない場合.
家から病院まで \(\color{royalblue}{2}\) 通りの道があるが, そこから学校までは \(1\) 本道.
家から薬局まで \(\color{magenta}{3}\) 通りの道があるが, そこから学校までは \(1\) 本道.
このとき, 通学路の総数は
\(\color{royalblue}{2}+\color{magenta}{3}=5\ [通り]\)
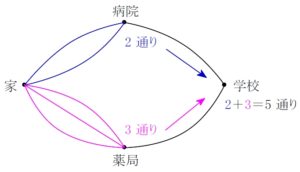
この例では, 病院経由と薬局経由という場合分けが発生していて, それらをトータルするためにたし算をしているんだ.
場合分けのあとは足し算
これが 「和の法則」.
場合分けというのは, それらの場合が同時にあるいは連続して起こることはない.
これが先ほどの 「積の法則」 との違い.
実際に問題を解くときは,
スタート地点からそこまで何通りの経路があるかを各地点に書き込んでいく
のがよいだろう.
そして,
合流地点で足し算
だ.
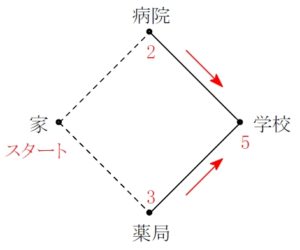
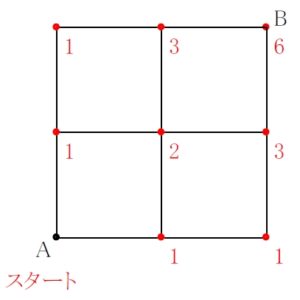
「田」 の字の街路の左下の角の地点 A から右上の角の地点 B までの最短経路数を, 各地点に書き込みながら求めてみよう.
まず, A の右隣の地点に注目.
A からそこまで最短で行く方法は \(1\) 通りしかないので, そこに \(\color{red}{1}\) と書き込む.
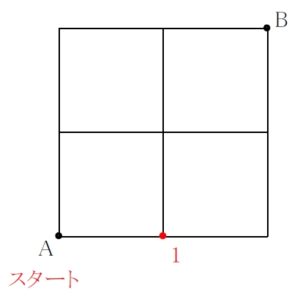
同様に, A からそこまで \(1\) 本道しかないという地点すべてに \(\color{red}{1}\) を書き込む.
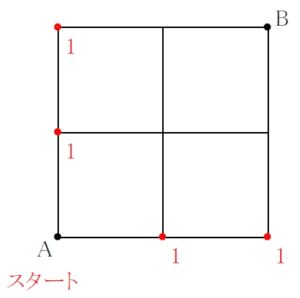
「田」 の真ん中の地点に着目. 合流地点でたし算.
左からくる \(\color{red}{1}\) 通りと下からくる \(\color{red}{1}\) 通りを加えて, A からそこまで \(\color{red}{2}\) 通り.
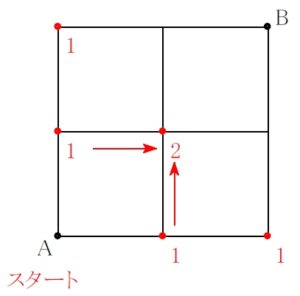
その右隣の地点は, 左からくる \(\color{red}{2}\) 通りと下からくる \(\color{red}{1}\) 通りを加えて, A からそこまで \(\color{red}{3}\) 通り.
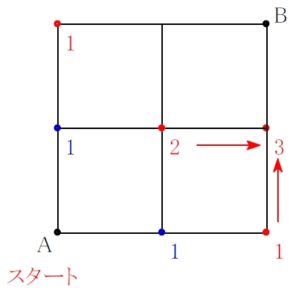
このとき, A の上の \(\color{royalblue}{1}\) や A の右の \(\color{royalblue}{1}\) は加える必要はない.
真ん中の 「\(\color{red}{2}\) 通り」 の中にすでに吸収されているからだ.
こうして B 地点まですべて書き込んでいくと, 最短経路の総数は \(\color{red}{6}\) 通りだということがわかるね.
■最短経路数と組合せ■
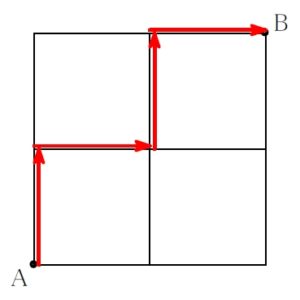
上の 「田」 の最短経路の \(1\) つに
↑ → ↑ →
と進む経路がある.
全 \(6\) 通りの経路は
→ → ↑ ↑
→ ↑ → ↑
→ ↑ ↑ →
↑ → → ↑
↑ → ↑ →
↑ ↑ → →
で, いずれも, 「→」 という移動 \(2\) 回と 「↑」 という移動 \(2\) 回の計 \(4\) 回の移動で構成されているね.
計 \(4\) 回の移動のうち何回目が 「→」 であるかに着目すると, \(6\) 通りの経路は,
\(1\) 回目と \(2\) 回目が 「→」
\(1\) 回目と \(3\) 回目が 「→」
\(1\) 回目と \(4\) 回目が 「→」
\(2\) 回目と \(3\) 回目が 「→」
\(2\) 回目と \(4\) 回目が 「→」
\(3\) 回目と \(4\) 回目が 「→」
と表現できる.
\(4\) 回中どの \(2\) 回が 「→」 であるかで
\(\displaystyle{}_{4}C_{2}=\frac{4\times3}{2\times1}=6\ [通り]\)
と計算することもできるということだ.
■通行止めがある場合■
先に出てきた, 病院経由・薬局経由の場合分けの通学路をもう一度考えよう.
病院から学校までの道が通行止めだったらどうなるか.
病院経由で学校まで来ることはありえなくなるので, 「\(\color{royalblue}{0}\) 通り」 とカウントする.
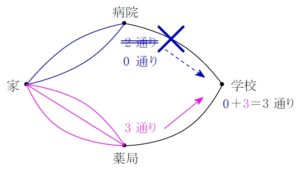
家から学校までの通学路の総数は,
\(\color{royalblue}{0}+\color{magenta}{3}=3\ [通り]\)
となる.
SPONSORED LINK
●例題 <最短経路数>●
図のような街路について, 次の場合の最短経路数を求めよ.
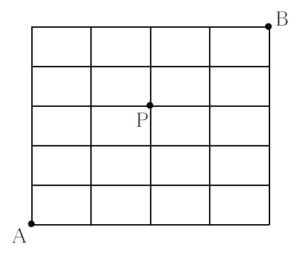
\((1)\) A 地点から B 地点まで行く
\((2)\) A 地点から, P 地点を通って B 地点まで行く
\((3)\) A 地点から, P 地点を通らずに B 地点まで行く
●解答 <和の法則>●
A からそこまでの最短経路が何通りあるかを書き込んでいく.
\((1)\)
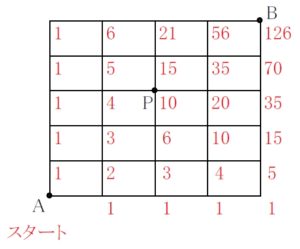
答 \(126\) 通り
\((2)\)
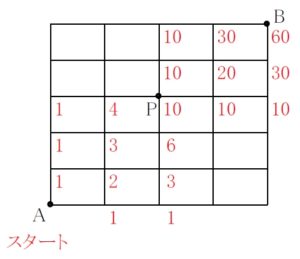
答 \(60\) 通り
\((3)\)
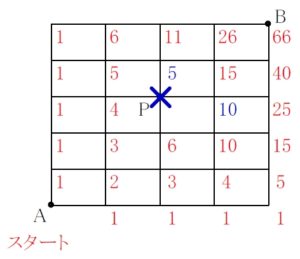
答 \(66\) 通り
●別解 <組合せ・積の法則>●
\((1)\) A から B までの最短経路は, \(4\) 回の「→」 と \(5\) 回の 「↑」 の計 \(9\) 回の移動で構成される.
\(9\) 回中どの \(4\) 回が 「→」 であるかで
\(\displaystyle{}_{9}C_{4}=\frac{9\times8\times7\times6}{4\times3\times2\times1}=126\ [通り]\)
答 \(126\) 通り
\((2)\) A から P までの最短経路は, \(2\) 回の「→」 と \(3\) 回の 「↑」 の計 \(5\) 回の移動で構成される.

\(5\) 回中どの \(2\) 回が 「→」 であるかで
\(\displaystyle{}_{5}C_{2}=\frac{5\times4}{2\times1}=10\ [通り]\)
また, P から B までの最短経路は, \(2\) 回の「→」 と \(2\) 回の 「↑」 の計 \(4\) 回の移動で構成される.