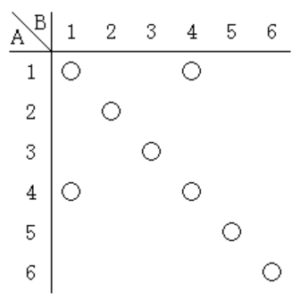
準備として, 順列・組合せ , 最短経路数 をしっかり理解しておきましょう.
■ダランベールの誤り■
「(数学の) 確率って何?」 と聞かれて,
\(\displaystyle確率=\frac{ある事柄が起こる場合の数}{起こりうるすべての場合の数}\)
としか答えられないようでは, 実は確率について何もわかっていないのと同じだ.
バカ正直に上の式にしたがって,
「\(2\) 個の白玉と \(1\) 個の赤玉が入った袋から無作為に \(1\) 個の玉を取り出すとき, それが白玉である確率」
を求めてみよう.
まず, 分母の, 起こりうるすべての場合は
「白玉が出る」, 「赤玉が出る」 の \(2\) 通り.
このうち, 白玉が出るのは \(1\) 通り.
よって, 確率は \(\displaystyle\frac{1}{2}\) … ???
なわけないよね!
これと同じような誤りを, ダランベール (フランス, \(1717\)~\(1783\)) という大数学者でもやらかした.
上の考え方の何がいけなかったのか. 次で説明しよう.
■確率 って?■
そもそも, 確率というものを計算するための前提条件がある.
\(\displaystyle\frac{ある事柄が起こる場合の数}{起こりうるすべての場合の数}\)
という式の分母に注目!
この 「起こりうるすべての場合」 が
同様に確からしい (どれが起こることも同じ程度に期待できる)
ことが大前提だ.
上の例は, 「白玉が出る」 と 「赤玉が出る」 が同様に確からしいとはいえないのに, 強引に式に当てはめているのが誤りの原因だ.
ダランベールだかカマンベールだか知らないが,
このような誤りを防ぐにはどうしたらいいと思う?
簡単な方法がある.
確率の問題で, 「\(2\) 個の白玉」 みたいな 「見分けがつかないもの」 が出てきたら,
見分けがつかずとも区別せよ!
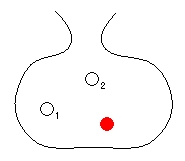
\(2\) 個の白玉に番号 「\(1\)」 「\(2\)」 などをつけて区別し, 「\(1\)」 が出る場合と 「\(2\)」 が出る場合はまったく別の結果とみなすんだ.
すると, 起こりうるすべての場合は
「白玉 \(1\) が出る」, 「白玉 \(2\) が出る」, 「赤玉が出る」 の \(3\) 通り
で, どの場合も 同様に確からしい.
このうち, 白玉が出るのは \(2\) 通り.
よって, 正しい確率は \(\displaystyle\frac{2}{3}\) となる.
■Point <確率>■
\(\displaystyle\frac{ある事柄が起こる場合の数}{起こりうるすべての場合の数}\)
全事象 (分母) は 同様に確からしい 状態に.
\(\longrightarrow\) 見分けつかずとも 区別 せよ.
●例題 1 <玉と確率>●
\(2\) 個の白玉と \(3\) 個の赤玉が入った袋から無作為に \(2\) 個の玉を取り出すとき, それらの色が異なる確率を求めよ.
●解答●

すべての取り出し方の総数は, 区別された \(5\) 個の玉から \(2\) 個を選ぶ組合せの総数
\({}_{5}C_{2}=\displaystyle\frac{5\times4}{2\times1}=10\) [通り]
で, どの場合も 同様に確からしい.
このうち, \(2\) 個の玉の色が異なる取り出し方の総数は, \(2\) 個の白玉から \(1\) 個を選び, \(3\) 個の赤玉から \(1\) 個を選ぶ組合せの総数であり,
\({}_{2}C_{1}\times{}_{3}C_{1}=2\times3=6\) [通り]
よって, 求める確率は,
\(\displaystyle\frac{6}{10}=\frac{3}{5}\)
答 \(\displaystyle\frac{3}{5}\)
慣れてきたら
\(\displaystyle\frac{{}_{2}C_{1}\times{}_{3}C_{1}}{{}_{5}C_{2}}=\frac{2\times3}{10}=\frac{3}{5}\)
と計算すればよいでしょう.
SPONSORED LINK
●例題 2 <さいころと確率>●
\(2\) 個のさいころを振ったとき, 出た目の数の積が平方数 (自然数の \(2\) 乗) である確率を求めよ.
●解答●
\(2\) 個のさいころを A, B として 区別する.
すべての目の出かたは,
\(6^2=36\) [通り]
で, どの場合も 同様に確からしい.