母 「こないだのテスト, 何点だったのよ.」
俺 「\(100_{(3)}\) 点でした .」

● 記数法って? ●
その名の通り, 数を記 (しる) す方法のこと.
参考書などでは 「\(n\) 進法」 と書いてあることもある.
日頃みんなが使っている 「\(5\)」 や 「\(198\)」 などの表記は,
数の表し方の \(1\) つであって, それがすべてではないんだ.
ではまず, 最もおなじみの \(10\) 進法から理解していこう.
● 10 進法って? ●
小銭が増えすぎて財布がパンパンに膨らむの, いやだよね?
\(1\) 円玉が \(10\) 枚あったら, ただちに \(10\) 円玉 \(1\) 枚に替えたい.
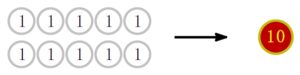
そして, \(10\) 円玉 \(10\) 枚で \(100(=10^2)\) 円玉に.

さらに, \(100\) 円玉 \(10\) 枚で \(1000(=10^3)\) 円札に.
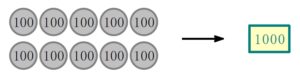
\(\cdots\cdots\)
このように
「\(\color{red}{10}\) 個で \(\color{red}{1}\) つに」
というのが \(\large\color{red}{10\ 進法}\) の基本理念だ.
例えば, ここに \(1\) 円玉が \(198\) 枚あったとしよう.
これを \(10\) 進法で 「両替」 していくと,
\(\color{red}{1}\) 枚の \(100\) 円玉, \(\color{red}{9}\) 枚の \(10\) 円玉, \(\color{red}{8}\) 枚の \(1\) 円玉となるね.

この表し方は \(0\) の個数が多くなると書くのが大変なので, 硬貨の種類を \(10\) の累乗で表すと,
\(\color{red}{1}\times 10^2 +\color{red}{9}\times 10 +\color{red}{8}\times 1\)
(もし 「\(10000000\)」 なら 「\(10^7\)」のほうが楽でしょう?)
そして, さらに \(10\) の累乗まで省いて略記したのが,
\(\color{red}{198}\)
という表記だ.
これは \(\large\color{red}{位取り記数法}\) といって,
硬貨の種類 (\(10\) の累乗) を省略する代わりに, それを数字の 「位置」 によって表現しているんだ.
\(\color{red}{8}\) が \(1\) 円玉の枚数であることは, その数字を \(1\) 番右の位に置くことで表し, これを \(1\) の位とよぶ.
\(\color{red}{9}\) が \(10\) 円玉の枚数であることは, その数字を右から \(2\) 番目の位に置くことで表し, これを \(10\) の位とよぶ.
\(\color{red}{1}\) が \(100(=10^2)\) 円玉の枚数であることは, その数字を右から \(3\) 番目の位に置くことで表し, これを \(100(=10^2)\) の位とよぶ.
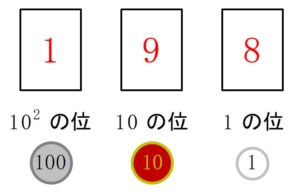
普段 慣れ親しんでいる数字の表し方は, いわば 究極の略記法 なのだ.
なお, 各位の数字として \(0\) ~ \(9\) 以外の数字がくることはない.
ある硬貨が \(10\) 枚以上になると, ただちに上位の硬貨に両替されるからだ.
● 3 進法を考えよう ●
そもそもなぜ僕らが数をかぞえるときに \(10\) を基礎にするのかというと,
おそらくヒトの手の指の本数が \(10\) 本だったからだろう.
では, もし宇宙のどこかに \(3\) 本指の知的生命体がいたら…

\(1\) 円玉 (日本円を使っているとは思えないが) \(3\) 枚でもう財布が重い.
\(3\) 本指で重いの持てないので, \(3\) 円玉に替えたい.
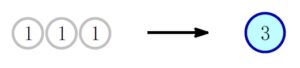
そして, \(3\) 円玉 \(3\) 枚で \(9(=3^2)\) 円玉に.
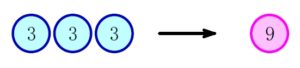
さらに, \(9\) 円玉 \(3\) 枚で \(27(=3^3)\) 円玉に.
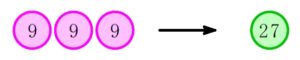
\(\cdots\cdots\)
このように
「\(\color{red}{3}\) 個で \(\color{red}{1}\) つに」
というのが \(\large\color{red}{3\ 進法}\) の考え方だ.
ここに \(19\) 枚の \(1\) 円玉がある.

これを \(3\) 本指宇宙人の気持ちになって両替してみよう.
\(19\) 枚を \(3\) 枚ずつセットにしていくと,
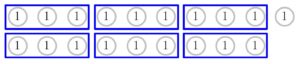
\(19=3\times6+\color{red}{1}\) (\(19\div3=6\cdots\color{red}{1}\)) \(\cdots\) ①
だから, \(6\) セットできて, \(1\) 円玉は \(\color{red}{1}\) 枚余る.
\(1\) 円玉 \(3\) 枚セットを \(3\) 円玉に替えると,
![]()
この時点では \(6\) 枚の \(3\) 円玉と \(\color{red}{1}\) 枚の \(1\) 円玉になる.
① の余り \(\color{red}{1}\) が, \(3\) 進法での \(1\) の位の数字 (\(1\) 円玉の枚数) を表している.
次に, この \(6\) 枚の \(3\) 円玉を \(3\) 枚ずつセットにしていくと,
![]()
\(6=3\times2+\color{red}{0}\) (\(6\div3=2\cdots\color{red}{0}\)) \(\cdots\) ②
だから, \(2\) セットできて, \(3\) 円玉は \(\color{red}{0}\) 枚余る.
\(3\) 円玉 \(3\) 枚セットを \(9\) 円玉に替えると,
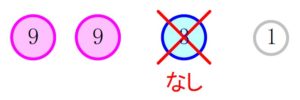
この時点では \(2\) 枚の \(9\) 円玉, \(\color{red}{0}\) 枚の \(3\) 円玉, \(\color{red}{1}\) 枚の \(1\) 円玉になる.
② の余り \(\color{red}{0}\) が, \(3\) 進法での \(3\) の位の数字 (\(3\) 円玉の枚数) を表している.
さらに, この \(2\) 枚の \(9\) 円玉を \(3\) 枚ずつセットにしていくと,

\(2=3\times0+\color{red}{2}\) (\(2\div3=0\cdots\color{red}{2}\)) \(\cdots\) ③
だから, \(0\) セットできて, \(9\) 円玉は \(\color{red}{2}\) 枚余る.
\(27(=3^3)\) 円玉以上への両替する硬貨はもうないので,
\(\color{red}{2}\) 枚の \(9(=3^2)\) 円玉, \(\color{red}{0}\) 枚の \(3\) 円玉, \(\color{red}{1}\) 枚の \(1\) 円玉で両替完了.
③ の余り \(\color{red}{2}\) が, \(3\) 進法での \(3^2\) の位の数字 (\(9\) 円玉の枚数) を表している.
結局, \(19\) 枚の \(1\) 円玉を \(3\) 進法両替した結果は,
![]()
つまり,
\(\color{red}{2}\times 3^2 +\color{red}{0}\times 3 +\color{red}{1}\times 1\)
さらに略記するため, \(3\) の累乗まで省いて,
\(\color{red}{201}_{(3)}\)
と表す.
これが \(3\) 進法の位取り記数法だ.
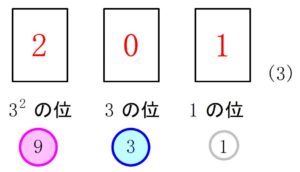
「\( _{(3)}\)」 は \(10\) 進法などと区別するために付す.
なお, 各位の数字として \(0\), \(1\), \(2\) 以外の数字がくることはない.
ある硬貨が \(3\) 枚以上になると, ただちに上位の硬貨に両替されるからだ.
さらに余計なことを言っておこう.
\(3\) 進法に 「\(6\) 円玉」 とかはないぞ.
それだと \(3\) 円玉 \(2\) 個で \(1\) つにしていて, 「\(3\) 個で \(1\) つに」 という \(3\) 進法の理念に沿ってない.
ところで, \(3\) 進法で表された正の整数を小さい順に並べてみよう.
めんどいので 「\( _{(3)}\)」 を省くよ.
\(1\), \(2\), \(10\), \(11\), \(12\), \(20\), \(21\), \(22\), \(100\), \(101\), \(102\), \(110\), \(111\), \(112\), \(120\), \(121\), \(122\), \(200\), \(201\), \(202\), \(210\), \(211\), \(212\), \(220\), \(221\), \(222\), \(1000\), \(1001\), \(\cdots\)
いつもの並び \(1\), \(2\), \(\color{gray}{3}\), \(\color{gray}{4}\), \(\color{gray}{5}\), \(\color{gray}{6}\), \(\color{gray}{7}\), \(\color{gray}{8}\), \(\color{gray}{9}\), \(10\), \(11\), \(12\), \(\color{gray}{13}\), \(\cdots\) において \(\color{gray}{3}\) \(\color{gray}{~}\) \(\color{gray}{9}\) を含む数を除外したものになっているのがわかるね.
それから数えてみて!
\(19\) 番目に例の \(201\) があるよ.
● 記数法の変換 ●
\(10\) 進法の \(19(=1\times 10+9\times 1)\) を \(3\) 進法に変換したものが \(\color{red}{201}_{(3)}\) で,
この各位の数字は, 割り算 ①, ②, ③ の余りだったよね.
そう, \(10\) 進法から \(3\) 進法への変換は, \(3\) で割っていったときに出てくる余りを \(1\) の位から順に並べればいい.
実際は商と余りを下へと書いていって, 余りを 「逆さ読み」 すればいいんだ.
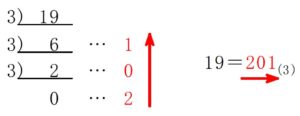
(例えば 「\(5\) 個で \(1\) つに」 の \(5\) 進法に直したいなら, \(5\) で割った余りを逆さ読み.)
逆に, \(3\) 進法の \(\color{red}{201}_{(3)}\) を \(10\) 進法に変換することは,
\(3\) 本指宇宙人の両替をくずして, 僕ら地球人の両替をすることを意味する.
そのためには, 両者の共通の硬貨である \(\color{red}{1}\) 円玉にくずして考える んだ.
先に見た通り, \(\color{red}{201}_{(3)}\ [円]\) は \(1\) 円玉にして \(19\) 枚分の価値があるんだけど,
この変換をするには次のように計算すればいいぞ.
\(\color{red}{201}_{(3)}\)
\(=\color{red}{2}\times 3^2 +\color{red}{0}\times 3 +\color{red}{1}\times 1\)
\(=\color{red}{2}\times 9 +\color{red}{0}\times 3 +\color{red}{1}\times 1\)
\(=18+0+1\)
\(=19(=1\times 10+9\times 1)\)
ちなみに \(5\) 進法の \(\color{red}{201}_{(5)}\) だと ぜんぜん価値が違ってくる.
「\(5\) 個で \(1\) つに」 という考えなので, 硬貨は \(1\) 円玉, \(5\) 円玉, \(25(=5^2)\) 円玉, \(\cdots\) となり,
\(1\) 円玉にして何枚分の価値があるかというと,
\(\color{red}{201}_{(5)}\)
\(=\color{red}{2}\times 5^2 +\color{red}{0}\times 5 +\color{red}{1}\times 1\)
\(=\color{red}{2}\times 25 +\color{red}{0}\times 5 +\color{red}{1}\times 1\)
\(=50+0+1\)
\(=51(=5\times 10+1\times 1)\)
となるね.
Point <記数法の変換> ★★★
\([1]\) \(n\) 進 → \(10\) 進
各位の数字に \(\color{red}{n}\) の累乗を掛けて足す
(\(1\) 円玉にくずす)
\([2]\) \(10\) 進 → \(n\) 進
\(\color{red}{n}\) で割った余りを逆さ読み
(\(n\) 個で \(1\) セットにしていく)
SPONSORED LINK
■ 例題 1 ■ <記数法の変換 (10進へ)>
\(5\) 進法の \(2034\) を \(10\) 進法で表せ.
■ 解答 ■
\(\color{red}{2034}_{(5)}\)
\(=\color{red}{2}\times5^3+\color{red}{0}\times5^2+\color{red}{3}\times5+\color{red}{4}\times1\)
\(=\color{red}{2}\times125+\color{red}{0}\times25+\color{red}{3}\times5+\color{red}{4}\times1\)
\(=250+0+15+4\)
\(=269\ (=2\times10^2 +6\times10+9\times 1)\)
答 \(269\)
■ 例題 2 ■ <記数法の変換 (10進から)>
\(10\) 進法の \(59\) を \(3\) 進法で表せ.
■ 解答 ■
\(59=3\times19+\color{red}{2}\) (\(59\div3=19\cdots\color{red}{2}\))
\(19=3\times6+\color{red}{1}\) (\(19\div3=6\cdots\color{red}{1}\))
\(6=3\times2+\color{red}{0}\) (\(6\div3=2\cdots\color{red}{0}\))
\(2=3\times0+\color{red}{2}\) (\(2\div3=0\cdots\color{red}{2}\))

よって,
\(59=\color{red}{2012}_{(3)}\)
答 \(2012_{(3)}\)
母 「\(9\) 点!?」
俺 「…」