SPI3 のテストセンターで実施される検査の一つです.
● 構造的把握 って? ●
「おおざっぱにとらえること」 ではない.
「おおざっぱ」 とは 「細かいことは気にせず なんとなく」 ということであって,
「なんとなく」 とは 「直感に頼って」 ということだ.
そしてそれは, 現代文の選択肢問題を高確率で はずしまくる, 国語が苦手な人の解き方だ.
それでは試験用に作られた問題は解けない.
「直感」 は人それぞれで, 「主観」だ.
それで答えが出るなら, 問題の解答が複数存在することになる.
それは致命的な出題ミスというものだ.
出題ミスをなくすにはどうしたらいいか.
その解答が, 正解たる 「客観的な根拠」 をもつように問題を作ればよい.
論理的に正しく考えれば万人の答えが一致するように.
そういう問題の正解を求めるには, 「直感」 ではなく,
論理的に考えて, 客観的な根拠を探す
しかない.
構造的把握力検査で出題されるのはどのような問題なのかは次で説明しよう.
■ 例題 1 ■ <文章題の構造>
次の ア ~ エ の中から, 問題の構造が似ているもの を \(2\) つ選べ.
ア はるおくんは \(150\) 円, あきおくんは \(70\) 円持っています. \(2\) 人合わせていくら持っていますか.
イ \(70\) 円のお菓子を買うのに \(150\) 円出したら, おつりはいくらですか.
ウ はるおくんは分速 \(150\ \rm m\), あきおくんは分速 \(70\ \rm m\) で, ある地点を同時に出発して一直線に同じ方向に進みます. 出発してから \(10\) 分後に \(2\) 人はどれだけ離れていますか.
エ なつこさんは \(20\) 歳, ふゆこさんは \(19\) 歳です. \(2\) 人の年齢の和は何歳ですか.
■ 解答 ■
問題を解くプロセスまたは計算式が同じになるもの を選ぶ.
問題文中に登場する名詞や数字は関係ない.
また, 実際に各問題を解き切る必要はない.
ア \(150+70\) で 「\(a+b\) 型」.
イ \(150-70\) で 「\(a-b\) 型」.
ウ はるおくんは \(1\) 分で \(150\ \rm m\) 進み, あきおくんは \(1\) 分で \(70\ \rm m\) 進む.
\(1\) 分で \(150-70(=80)[\rm m]\) 離れる.
\(10\) 分で \((150-70)\times10\ (=80\times10)[\rm m]\) 離れている.
「\((a-b)\times c\) 型」.
エ \(20+19\) で 「\(a+b\) 型」.
答 ア と エ
そもそも, 「問題の構造」 とは何かを定義していないので, 問題として成立していない気がしますけどね.
問題文とともに空気を読んで, 上のような解釈をすればこの答えになります.
■ 例題 2 ■ < 2 文の関係による分類>
次の ア ~ オ を, 指示に従って \(\rm P\) (\(2\) つ) と \(\rm Q\) (\(3\) つ) に分けるとき, P に分類されるものはどれか.
指示: ア ~ オ は, \(2\) つのことがらの関係についての記述である. その 関係性の違い によって, \(\rm P\) と \(\rm Q\) の \(2\) グループに分けなさい.
ア ちゃんと勉強すれば, 満点とれるよ.
イ 私が鳥なら, あなたのもとへ飛んでゆく.
ウ \(1\) ヶ月たったら, 忘れちゃう.
エ 俺が死んだら, 遺産は全部くれてやる.
オ どんな願いも叶うなら, \(3\) 歳くらいから人生やり直す.
■ 解答 ■
「条件 (~のとき) / 結果」 : ア, ウ, エ \(\cdots\) \(\rm Q\)
ア 「ちゃんと勉強したとき / 満点とれるよ」
ウ 「\(1\) ヶ月たったとき / 忘れちゃう」
エ 「俺が死んだとき / 遺産は全部くれてやる」
「仮定 (もし~なら) / 結論」 : イ, オ \(\cdots\) \(\rm P\)
イ 「もし私が鳥なら / あなたのもとへ飛んでゆく」
オ 「もしどんな願いも叶うなら / \(3\) 歳くらいから人生やり直す」
※ 英語の 「仮定法」 のように, 仮定では, 話者は述べたことが起こりえないと思っています.
答 イ と オ
彼は \(3\) 歳のとき何をやらかしたんでしょうね\(\cdots\)
■ 例題 3 ■ <文の内容による分類>
次の ア ~ オ を, 指示に従って \(\rm P\) (\(2\) つ) と \(\rm Q\) (\(3\) つ) に分けるとき, P に分類されるものはどれか.
指示: ア ~ オ は, 子供が将来について答えたものである. 答えの種類 によって, \(\rm P\) と \(\rm Q\) の \(2\) グループに分けなさい.
ア 親孝行な子でありたい.
イ いつか 「ゴミ」 という言葉が存在しないクリーンでエコな世の中になってほしい.
ウ 山賊王に おれはなる.
エ 研究者になって, 好きな人と手をつないでも手汗が出ない薬を開発する.
オ 「もみあげカールが最高のステータス」 という社会になるといいな.
■ 解答 ■
「意志 (~しよう)」 : ア, ウ, エ \(\cdots\) \(\rm Q\)
ア 「親孝行な子でいよう」
ウ 「山賊王になろう」
エ 「好きな人と手をつないでも手汗が出ない薬を開発しよう」
切実か!
「願望 (~てほしい)」 : イ, オ \(\cdots\) \(\rm P\)
イ 「クリーンでエコな世の中になってほしい」
オ 「もみあげカールが最高という社会になってほしい」
政治家になって もみあげカール優遇法案 を通してください.
答 イ と オ
● <確認> 命題の 逆・裏・対偶 ●
詳しくは 「命題」 のページ参照.
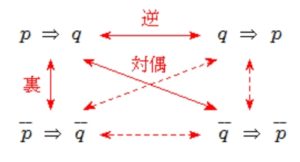
逆は, もとの命題と真偽が一致するとは限らない.
裏も, もとの命題と真偽が一致するとは限らない.
対偶どうしの真偽は一致する.
例えば, 「変更あれば連絡します (\(p\Longrightarrow q\))」
と, 「連絡なければ変更なし (\(\overline{q}\Longrightarrow\overline{p}\))」
は意味内容が同じなので, 真偽が一致して当然だ.
■ 例題 4 ■ <真偽の一致による分類>
次の ア ~ オ を, 指示に従って \(\rm P\) (\(2\) つ) と \(\rm Q\) (\(3\) つ) に分けるとき, P に分類されるものはどれか.
指示: ア ~ オ は命題である. その 真偽の一致 によって, \(\rm P\) と \(\rm Q\) の \(2\) グループに分けなさい. ただし, 怠け者でない者は努力家であり, 努力家は怠け者でないとする.
ア 努力家ならば成功者だ.
イ 成功者ならば努力家だ.
ウ 努力家でないならば成功者でない.
エ 成功者でないならば努力家でない.
オ 怠け者ならば成功者でない.
■ 解答 ■
成功者, 努力家, 怠け者をそれぞれ 「\(成\)」, 「\(努\)」, 「\(怠\)」 と表す.
指示にある ただし書きは, 「\(\overline{怠}\)」 と 「\(努\)」 が同一のものであることを示している.
これを,
① \(\overline{怠}=努\)
と表すことにする.
また,
ア \(努\Longrightarrow成\)
イ \(成\Longrightarrow努\)
ウ \(\overline{努}\Longrightarrow\overline{成}\)
エ \(\overline{成}\Longrightarrow\overline{努}\)
オ \(怠\Longrightarrow\overline{成}\)
である.
このうち, 真偽が一致するものどうしをグループにする.
ア, エ \(\cdots\) \(\rm P\)
ア と エ は対偶どうしなので, 真偽が一致する.
イ, ウ, オ \(\cdots\) \(\rm Q\)
イ と ウ は対偶どうしなので, 真偽が一致する.
オ の対偶は \(成\Longrightarrow\overline{怠}\) であり, ① より, \(成\Longrightarrow努\) と書ける.
これは イ と同じ命題なので真偽が一致する.
答 ア と エ
各命題が真なのか偽なのかは, 問題文の条件からは判断できません.
判断できるのは, あくまで, 真偽が 「一致するか否か」です.
間違っても, 個人の経験や感情で真偽そのものを確定させようと考えてはいけません.
● <確認> 三段論法 ●
詳しくは 「命題」 のページ参照.
「\(\color{red}{p} \Longrightarrow q\)」, 「\(q \Longrightarrow \color{red}{r}\)」 がともに真であるとき,
「\(\color{red}{p} \Longrightarrow \color{red}{r}\)」 も真になる.
例えば, 「人間ならば動物だ」, 「動物ならばいつか死ぬ」 がともに真であることから,
「人間ならばいつか死ぬ」 も真である.
なお,
「\(\color{red}{p} \Longrightarrow q\)」, 「\(\color{red}{r} \Longrightarrow q\)」 がともに真であっても,
\(\color{red}{p}\) と \(\color{red}{r}\) は 無関係.
例えば, 「\(\rm P\) さんは \(\rm Q\) さんを愛している」, 「\(\rm R\) さんも \(\rm Q\) さんを愛している」 がともに真であっても,
\(\rm P\) さんと \(\rm R\) さんが愛し合っていたり (三角関係), 同一人物だったり (二重人格) するとは限らない.
単に \(\rm Q\) さんがモテモテなだけだ.
■ 例題 5 ■ <論法の正しさによる分類>
次の ア ~ オ を, 指示に従って \(\rm P\) (\(2\) つ) と \(\rm Q\) (\(3\) つ) に分けるとき, P に分類されるものはどれか.
指示: ア ~ オ を 論法の正しさ によって, \(\rm P\) と \(\rm Q\) の \(2\) グループに分けなさい.
ア すべての人間は動物だ. すべての動物はいつか死ぬ. ゆえに, すべての人間はいつか死ぬ.
イ ちくわぶ が入ってないなら おでんではない. おでんには必ず大根が入っている. つまり, ちくわぶ は大根といえる.
ウ 友達ってなろうと思って なるんじゃない. 友達って気づいたときには なってるものなの. だからあたしたちは友達よ.
エ 国語が得意ならば論理力があり, 数学が得意ならば論理力がある. 数学が得意でない者は国語も得意でない.
オ いじめは人を傷つける. 人を傷つけるのは犯罪だ. だったらいじめは犯罪だ.
■ 解答 ■
論法が正しいものと, 正しくないものに分類する.
論法が正しい : ア, オ \(\cdots\) \(\rm P\)
ア 「\(\color{red}{人間}\Longrightarrow動物\)」,
「\(動物\Longrightarrow \color{red}{死ぬ}\)」
がともに真のとき,
「\(\color{red}{人間}\Longrightarrow \color{red}{死ぬ}\)」
も真だから, 論法が正しい.
(「\(\color{red}{p} \Longrightarrow q\)」, 「\(q \Longrightarrow \color{red}{r}\)」 がともに真のとき, 「\(\color{red}{p} \Longrightarrow \color{red}{r}\)」 も真.)
オ 「\(\color{red}{いじめ}\Longrightarrow傷つける\)」,
「\(傷つける\Longrightarrow \color{red}{犯罪}\)」
がともに真のとき,
「\(\color{red}{いじめ}\Longrightarrow \color{red}{犯罪}\)」
も真だから, 論法が正しい.
(「\(\color{red}{p} \Longrightarrow q\)」, 「\(q \Longrightarrow \color{red}{r}\)」 がともに真のとき, 「\(\color{red}{p} \Longrightarrow \color{red}{r}\)」 も真.)
論法が正しくない : イ, ウ, エ \(\cdots\) \(\rm Q\)
イ 「\(\overline{ちくわぶ入り}\Longrightarrow\overline{おでん}\)」 (対偶:「\(おでん\Longrightarrow \color{red}{ちくわぶ入り}\)」),
「\(おでん\Longrightarrow \color{red}{大根入り}\)」
がともに真であっても,
\(\color{red}{ちくわぶ}\) と \(\color{red}{大根}\) は 無関係. 論法が正しくない.
(「\(p \Longrightarrow \color{red}{q}\)」, 「\(p \Longrightarrow \color{red}{r}\)」 がともに真であっても, \(\color{red}{q}\) と \(\color{red}{r}\) は 無関係.)
ウ 「\(友達\Longrightarrow\overline{なろうと思ってなる}\)」,
「\(友達\Longrightarrow気づいたときには なってる\)」
がともに真であっても,
「\(あたしたち\Longrightarrow友達\)」
が真とは限らない. 論法が正しくない.
エ 「\(\color{red}{国語が得意}\Longrightarrow論理力がある\)」,
「\(\color{red}{数学が得意}\Longrightarrow論理力がある\)」
がともに真であっても,
\(\color{red}{国語が得意}\) と \(\color{red}{数学が得意}\) は 無関係. 論法が正しくない.
(「\(\color{red}{p} \Longrightarrow q\)」, 「\(\color{red}{r} \Longrightarrow q\)」 がともに真であっても, \(\color{red}{p}\) と \(\color{red}{r}\) は 無関係.)
答 ア と オ
● 学習法 ●
この構造的把握力検査, なかなか勉強しにくそうですよね.
コツが 2 つあります.
① 論理的な根拠 を意識して解くこと.
② 演習を 繰り返す こと.
① は, 言い換えると, 「ただ漫然と問題を解くのをやめる」 ということです.
先にも述べたように, 問題作成する側の姿勢として, 客観的な根拠がない選択肢を正解にする勇気がありません.
万人を説得しうる根拠を持ったものだけが正解になります.
そして, その根拠が見抜けるようにならない限り, つねに正答し続けることは不可能です.
「直感, センス, なんとなく」 (数学・国語ができない原因) を捨て去る意識改革が必要です.
② は同じ問題を繰り返し解け, ということを必ずしも意味するわけではありません.
問題演習すること自体を反復してくださいということです.
スポーツでもゲームでもなんでもそうですが, 頭で理論がわかっていても, それを実践しないと身につきませんよね.
① を担保しながら ② を実践する, というのが大事です. どっちが欠けてもダメです.
演習する際のおすすめ問題集を紹介しておきます.
『SPI3 構造的把握力検査 攻略ハンドブック』 (ブレスト研 編著) (以下にリンクあり)
特長は
・図による説明が分かりやすい
・基礎知識の説明, 周辺知識の解説が豊富
・解法の Point が明確
・演習問題量が充実
など, 賞賛すべき点がいろいろあります.
短所を挙げるとすれば, あまりに基本的な事項の解説は割愛している, ということでしょうか.
対偶の真偽はなぜ一致するのかとか, いわゆる順列・組合せ公式の成り立ちとかまでは書いてません.
ですので基本事項に関しては当サイト (数学Mass-Math) をご覧ください.
 |
SPI3「構造的把握力検査」攻略ハンドブック 2021年版/ブレスト研【1000円以上送料無料】 価格:1,320円 |
![]()