● 集合 って ? ●
「ものの集まり」 のこと.
集まっているものは, 物でも人でも数でも何でもいいんだ.
● 便利グッズ、ベン図 ●
集合の問題を解きやすくする便利グッズがある.
その名も \(\large\color{red}{ベン図}\) (Venn diagram).
おおげさに言っているが, 集合を丸や四角などで表した図のことだ.
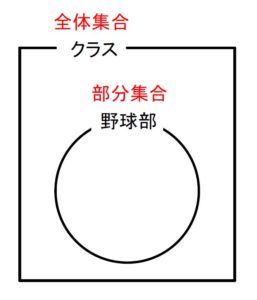
クラス全員の集合 (\(\large\color{red}{全体集合}\))と, その一部である野球部員の集合 (\(\large\color{red}{部分集合}\)) をこんなふうに表したりする.
ベン図は哲学者のジョン・ベンさん (John Venn, 英, 1834-1923) という人が考案したと言われている.
この人がジョン・ベン.

だれが〇ョンベンだ!
俺 ケンブリッジ大学だぞ なめんなよ.
という声が聞こえてきそうである.
● 共通部分 ●
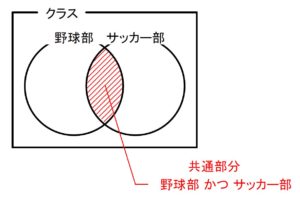
あるクラスで野球部とサッカー部を掛け持ちしているすごい人たちがいたとしよう.
この人たちは野球部員の集合に属し かつ サッカー部員の集合にも属す.
このような兼部をしている人たちの集合を, \(2\) つの集合の \(\large\color{red}{共通部分}\) という.
● 和集合 ●
日常で
「あの人は野球部 または サッカー部に入っている.」
と言われたら, ふつうはどっちか一方に所属していると解釈するよね.
ところが!
数学で 「または」 というときは兼部の人も含める.
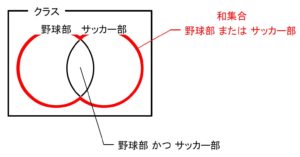
「野球部 または サッカー部」 とは野球部とサッカー部の少なくとも一方に属しているものの集合で,
これを \(2\) つの集合の \(\large\color{red}{和集合}\) という.
\(\color{red}{2}\) つの集合の共通部分も和集合に含まれるのだ.
● 雪だるま公式 ●
あるクラスに 野球部員 が \(\color{blue}{6}\) 人, サッカー部員 が \(\color{magenta}{8}\) 人, 共通部分 「野球部員 かつ サッカー部員」 が \(\color{purple}{3}\) 人 いたとしよう.

このとき, 和集合 「野球部員 または サッカー部員」 の人数を求めたい.
ベン図で見ると 雪だるま みたいな形をした部分の人数だ.
各部員を点 (●) で表し, カウントされたものにはチェック印を付けていく.
まず 野球部員 の \(\color{blue}{6}\) 人. \(6\) つのチェック印を付ける.
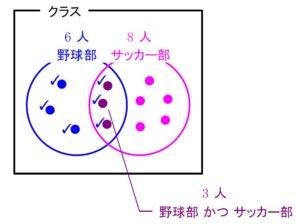
次に サッカー部員 の \(\color{magenta}{8}\) 人. さらに \(8\) つのチェック印を付ける.

ここまで合計 \(\color{blue}{6}+\color{magenta}{8}(=14)\) 個 付けたことになる.
しかしよく見ると, 兼部 の \(\color{purple}{3}\) 人 はダブルチェックしているため, \(\color{red}{3}\) 個を消す.
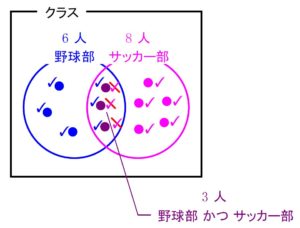
結果, \(\color{blue}{6}+\color{magenta}{8}-\color{red}{3}(=11)\) 個のチェック印を付けたことになる.
これこそが 「野球部員 または サッカー部員」 の人数だ.
これを一般化して, 「雪だるま公式」 とでも名付けておこう.
Point <集合> ★★★
\(\large\color{red}{ベン図}\) を描いて考える.
「雪だるま公式」
\(\large\color{red}{(A\ または\ B\ の人数)}\) \(\large\color{red}{=(A\ の人数)+(B\ の人数)}\) \(\large\color{red}{-(A\ かつB\ の人数)}\)
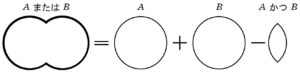
最後の引き算は ダブルチェック解消 のため.
SPONSORED LINK
■ 例題 ■ <集合>
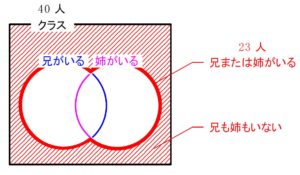
あるクラスの \(40\) 人のうち, 兄がいる人 は \(\color{blue}{15}\) 人, 姉がいる人 は \(\color{magenta}{13}\) 人, 兄も姉もいる人 は \(\color{purple}{5}\) 人 いる.
次のような人は何人いるか.
\((1)\) 兄はいるが姉はいない
\((2)\) 兄または姉がいる
\((3)\) 兄も姉もいない
■ 解答 ■
\((1)\)
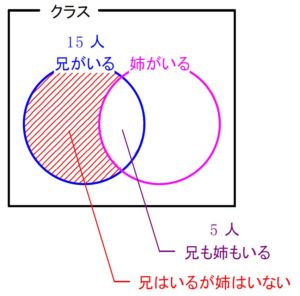
\(\color{blue}{15}-\color{purple}{5}=\color{red}{10}\ [人] \)
答 \(10\) 人
\((2)\)
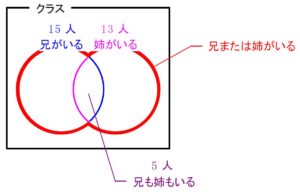
\(\color{blue}{15}+\color{magenta}{13}-\color{purple}{5}=\color{red}{23}\ [人] \)
答 \(23\) 人
\((3)\)