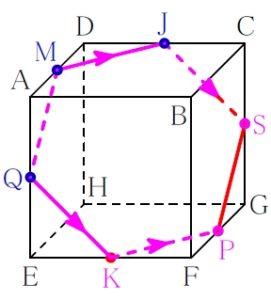
● 立方体の切断 ●
立方体の形をしたお豆腐があったとしよう.
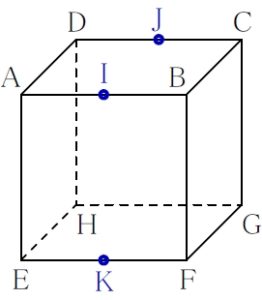
この立方体を \(\rm ABCD-EFGH\) とし, 諸事情により半透明であるとする.
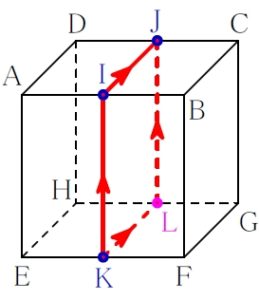
辺 \(\rm AB\), \(\rm CD\), \(\rm EF\) の中点をそれぞれ \(\color{royalblue}{\rm I}\), \(\color{royalblue}{\rm J}\), \(\color{royalblue}{\rm K}\) と名付ける.
この \(3\) 点を通るように縦にまっすぐ包丁を入れ, お豆腐を切り分ける.
切り口 (切断面の周) の図形は, ほぼ直観で正方形だとわかる.
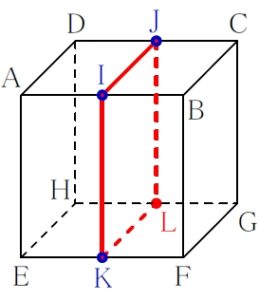
包丁は指定された \(3\) 点以外に, 辺 \(\rm GH\) の中点 \(\rm L\) も自動的に通過することもわかるだろう.
「当たり前じゃないか」と.
その当たり前から学べることはたくさんある.
この例から得られる, 立体の切り口のルール \(3\) つをまとめておこう.
ルール ① 「表面上の法則」:切り口は立体の表面上
これはむしろ切り口という語の定義そのものかもしれないが,
お豆腐の例でいうと, 切り口の作図をする際に点 \(\color{royalblue}{\rm J}\) と \(\color{royalblue}{\rm K}\) を結んではならない.
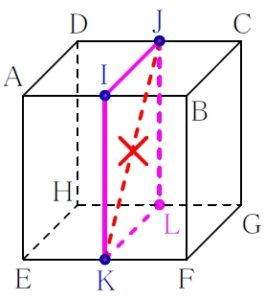
線分 \(\rm JK\) は立体の中を通過していくので, 切り口の線とはいえない.
ルール ② 「平行線の法則」:面が平行なら切り口も平行
立方体では, 向かい合う面どうしは平行だ.
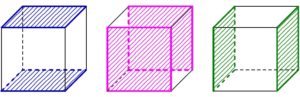
平行な面に現れる切り口の線は平行になる.
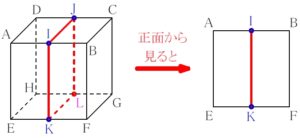
ルール ③ 「一直線の法則」:切断面は横から見ると一直線
お豆腐という名の立方体を包丁という名の平面で切っているわけだが,
その平面というのは, ある方向から見ると直線に見える.
つまり, 切断 「面」 もある角度から見れば \(1\) つの直線だ.
Point <切断面> ★★★
① 「表面上の法則」:切り口は立体の表面上
② 「平行線の法則」:面が平行なら切り口も平行
③ 「一直線の法則」:切断面は横から見ると一直線
SPONSORED LINK
● 四角形の種類 ●
切り口の図形の名前を正しく答えるには, 図形の名称と定義をしっかり覚えている必要がある.
そこで, とくに種類が多い四角形について整理しておこう.
台形 \(\cdots\) (少なくとも) \(1\) 組の対辺が平行な四角形.
平行四辺形 \(\cdots\) \(2\) 組の対辺が平行な四角形.
長方形 \(\cdots\) \(4\) つの角が等しい (つまり直角である) 四角形.
ひし形 \(\cdots\) \(4\) つの辺が等しい四角形.
正方形 \(\cdots\) \(4\) つの角が等しく, \(4\) つの辺が等しい四角形.
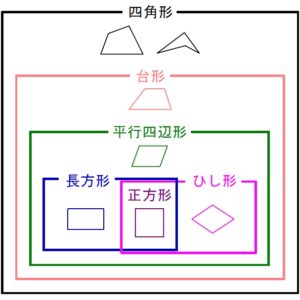
とくに, 線対称な形の台形は 等脚台形 とよばれる.
■ 例題 <立方体の切り口> ■
立方体 \(\rm ABCD-EFGH\) において, 辺 \(\rm AB\), \(\rm CD\), \(\rm EF\), \(\rm GH\), \(\rm AD\), \(\rm BC\), \(\rm EH\), \(\rm FG\), \(\rm AE\), \(\rm BF\), \(\rm CG\), \(\rm DH\) の中点をそれぞれ \(\color{magenta}{\rm I}\), \(\color{magenta}{\rm J}\), \(\color{magenta}{\rm K}\), \(\color{magenta}{\rm L}\), \(\color{magenta}{\rm M}\), \(\color{magenta}{\rm N}\), \(\color{magenta}{\rm O}\), \(\color{magenta}{\rm P}\), \(\color{magenta}{\rm Q}\), \(\color{magenta}{\rm R}\), \(\color{magenta}{\rm S}\), \(\color{magenta}{\rm T}\) とする.
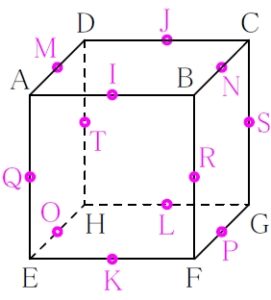
次の \(3\) 点を通る平面でこの立方体を切断したときの切り口の図形は何か.
最も適当なもの を解答群から選べ.
\((1)\) \(\color{royalblue}{\rm A}\), \(\color{royalblue}{\rm C}\), \(\color{royalblue}{\rm F}\)
\((2)\) \(\color{royalblue}{\rm A}\), \(\color{royalblue}{\rm D}\), \(\color{royalblue}{\rm F}\)
\((3)\) \(\color{royalblue}{\rm D}\), \(\color{royalblue}{\rm F}\), \(\color{royalblue}{\rm Q}\)
\((4)\) \(\color{royalblue}{\rm E}\), \(\color{royalblue}{\rm J}\), \(\color{royalblue}{\rm M}\)
\((5)\) \(\color{royalblue}{\rm D}\), \(\color{royalblue}{\rm K}\), \(\color{royalblue}{\rm P}\)
\((6)\) \(\color{royalblue}{\rm J}\), \(\color{royalblue}{\rm M}\), \(\color{royalblue}{\rm Q}\)
解答群
三角形 二等辺三角形 直角三角形
直角二等辺三角形 正三角形
四角形 台形 等脚台形 平行四辺形
長方形 ひし形 正方形
五角形 正五角形
六角形 正六角形
■ 解答 ■
ルールに従って切り口の線を作図していく.
\((1)\)
ルール ① 「表面上の法則」
\(\rm A\) と \(\rm C\) を結ぶと, これは立体の表面上だから切り口の線になる.
同様に, \(\rm A\) と \(\rm F\), \(\rm C\) と \(\rm F\) も結んでよい.
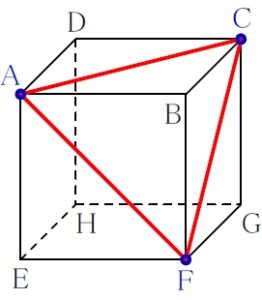
線分 \(\rm AC\), \(\rm CF\), \(\rm FA\) はすべて正方形の対角線で長さが等しい.
答 正三角形
※ ちなみに, \(\angle \rm AFC\) は正三角形の内角なので \(60^\circ\) です.
これを立方体の真上から見下ろすと, \(\angle \rm ABC\) に重なって見えるため \(90^\circ\) に見えます.
しかしこれはあくまで見かけの角度であって, 本当の角度は \(60^\circ\) です.
このように実際の角度と異なって見えるのは, 正三角形に対して 「斜めの方向」 から見ているからです.
\((2)\)
ルール ① 「表面上の法則」
\(\rm A\) と \(\rm D\), \(\rm A\) と \(\rm F\) は結んでよい.
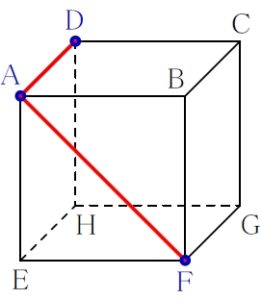
ルール ② 「平行線の法則」
面 \(\rm ABFE\) と面 \(\rm DCGH\) は平行なので, 現れる切り口の線も平行になる.
\(\rm AF\) に平行な線として \(\rm DG\) が引ける.
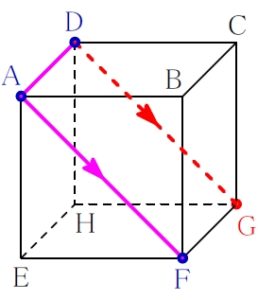
再び ルール ① 「表面上の法則」
\(\rm F\) と \(\rm G\) は結んでよい.
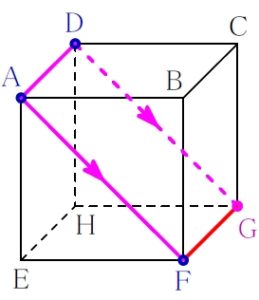
四角形 \(\rm ADGF\) はルール ② により平行四辺形で, とくに \(4\) つの角が等しいから長方形.
すべての辺が等しいわけではないので, 正方形ではない.
答 長方形
※ 長方形の \(2\) つの対角線の長さは等しくなります.
つまり, \(\rm AG=\rm DF\) です.
\((3)\)
ルール ① 「表面上の法則」
\(\rm D\) と \(\rm Q\), \(\rm Q\) と \(\rm F\) は結んでよい.
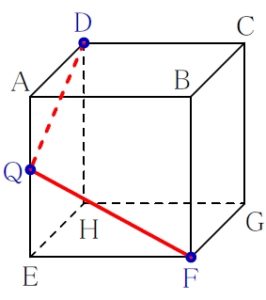
ルール ② 「平行線の法則」
面 \(\rm ABFE\) と面 \(\rm DCGH\) は平行なので, \(\rm QF\) に平行な線として \(\rm DS\) が引ける.
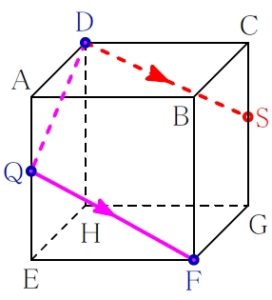
再び ルール ① 「表面上の法則」
\(\rm F\) と \(\rm S\) は結んでよい.
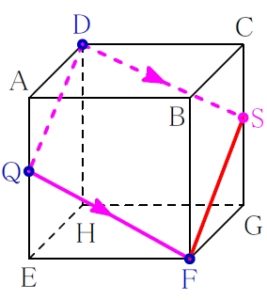
四角形 \(\rm DQFS\) は \(4\) 辺が等しいので ひし形.
内角は直角ではない (\((1)\) の \(\angle \rm AFC\) が直角ではないのと同じ理由) ので, 正方形ではない.
答 ひし形
※ \(4\) つの直角三角形 \(\triangle \rm ADQ\), \(\triangle \rm CDS\), \(\triangle \rm EFQ\), \(\triangle \rm GFS\) は合同なので,
\(\rm DQ=DS=FQ=FS\)
なお, ひし形は, 長方形のように \(2\) つの対角線の長さが等しいとは限りません.
実際, \(\rm DF\not=QS\) です.
\((4)\)
ルール ① 「表面上の法則」
\(\rm E\) と \(\rm M\), \(\rm M\) と \(\rm J\) は結んでよい.
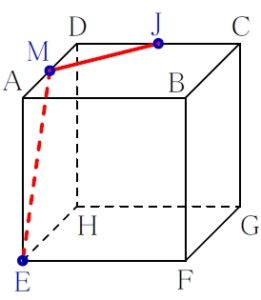
ルール ② 「平行線の法則」
面 \(\rm ABCD\) と面 \(\rm EFGH\) は平行なので, \(\rm MJ\) に平行な線として \(\rm EG\) が引ける.
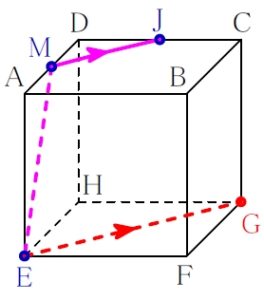
再び ルール ① 「表面上の法則」
\(\rm G\) と \(\rm J\) は結んでよい.
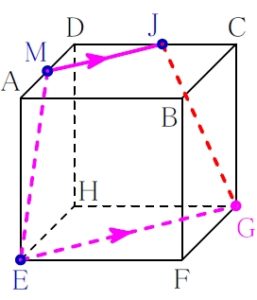
四角形 \(\rm EGJM\) は, \(\rm EG\) と \(\rm MJ\) は平行だが, \(\rm EM\) と \(\rm GJ\) は平行でないから, 平行四辺形でない台形.
\(\rm EM=GJ\) より等脚台形.
答 等脚台形
\((5)\)
ルール ① 「表面上の法則」
\(\rm P\) と \(\rm K\) は結んでよい.
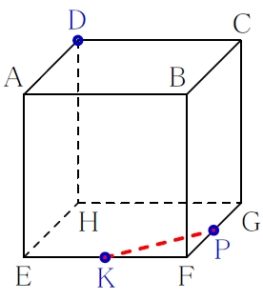
ルール ③ 「一直線の法則」
切断面が直線 (\(\rm DK\)) に見える方向から見ると,
切断面は辺 \(\rm AE\) 上の \(1\) 点 \(\rm U\) を通ることがわかる.
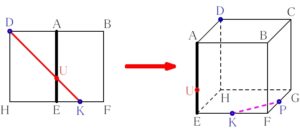
再び ルール ① 「表面上の法則」
\(\rm D\) と \(\rm U\), \(\rm U\) と \(\rm K\) は結んでよい.
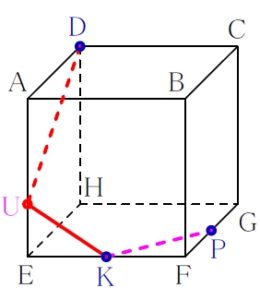
ルール ② 「平行線の法則」
面 \(\rm ABFE\) と面 \(\rm DCGH\) は平行なので, \(\rm UK\) に平行な線として \(\rm DV\) が引ける.
ただし, \(\rm V\) は辺 \(\rm CG\) 上の点.
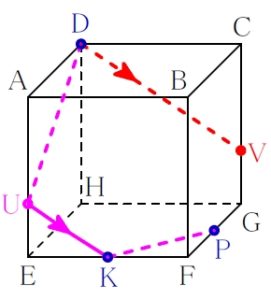
再び ルール ① 「表面上の法則」
\(\rm P\) と \(\rm V\) は結んでよい.
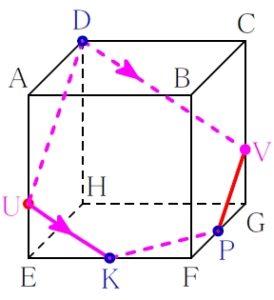
五角形 \(\rm DUKPV\) はすべての辺が等しいわけではないので, 正五角形ではない.
答 五角形
\((6)\)
ルール ① 「表面上の法則」
\(\rm J\) と \(\rm M\), \(\rm M\) と \(\rm Q\) は結んでよい.
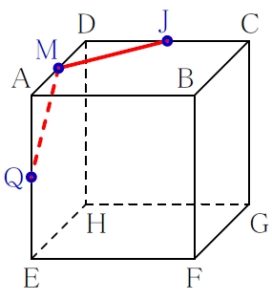
ルール ③ 「一直線の法則」
切断面が直線 (\(\rm MQ\)) に見える方向から見ると,
切断面は辺 \(\rm EF\) の中点 \(\rm K\) を通ることがわかる.
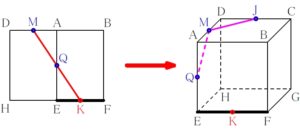
再び ルール ① 「表面上の法則」
\(\rm Q\) と \(\rm K\) は結んでよい.
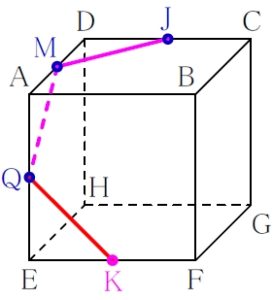
ルール ② 「平行線の法則」
面 \(\rm ABCD\) と面 \(\rm EFGH\) は平行なので, \(\rm MJ\) に平行な線として \(\rm KP\) が引ける.
面 \(\rm ABFE\) と面 \(\rm DCGH\) は平行なので, \(\rm QK\) に平行な線として \(\rm JS\) が引ける.
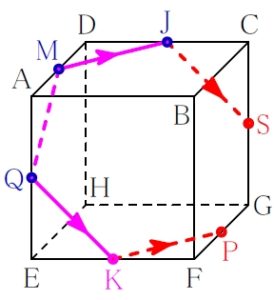
再び ルール ① 「表面上の法則」
\(\rm P\) と \(\rm S\) は結んでよい.