● 損益算 って? ●
商品を売ったときに生じる利益や損失に関する, 割合の問題.
原価 (仕入れ値) \(100\) 円のりんごを \(100\) 円で売ったら, ただのボランティアだ.
ふつう利益を上乗せして, \(120\) 円とかを定価として売るだろう.
この定価で売れた場合, 差額
\(120-100=20\ [円]\)
が利益.
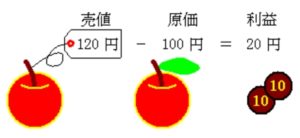
つまり,
\(\color{red}{(利益)=(売値)-(原価)}\)
(利益がマイナスのときは 「損失」)
ところで,
\(\displaystyle20=100\color{red}{\times\frac{2}{10}}\)
だから, 利益の \(20\) 円は, 原価 \(100\) 円の \(\color{red}{2}\) 割 にあたる.
定価 \(120\) 円は,
「原価の \(\color{royalblue}{2}\) 割の利益を見込んで つけた定価」
であり,
「原価の \(\color{royalblue}{2}\) 割増」
の金額だ.
さらに,
\(\displaystyle120=100\color{royalblue}{\times\frac{12}{10}}\)
より, 定価 \(120\) 円は原価 \(100\) 円の \(\color{royalblue}{12}\) 割 にあたることがわかる.
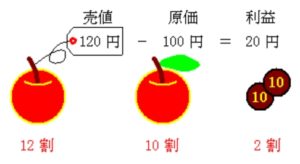
「\(\color{royalblue}{2}\) 割増」 とは 「もとの \(\color{royalblue}{12}\) 割」 \((10+2=12)\) だ.
「深夜料金 \(\color{royalblue}{2}\) 割増」 を電卓で計算するなら 「\(\color{royalblue}{\times1.2}\)」 でいい.
同じように考えて, 例えば
「\(\color{magenta}{1}\) 割引」 とは 「もとの \(\color{magenta}{9}\) 割」 \((10-1=9)\) ね.
「タイムセールで \(10\%\) OFF」 なら, もとの \(90\%\) つまり \(\color{magenta}{9}\) 割 だから, 「\(\color{magenta}{\displaystyle\times\frac{9}{10}}\)」, 電卓では 「\(\color{magenta}{\times0.9}\)」 だ.
■ 例題 1 <利益の計算> ■
原価 \(1000\) 円の品物に \(\color{royalblue}{2}\) 割の利益を見込んで 定価をつけたが, 売れなかったので定価の \(\color{magenta}{1}\) 割引 で売った.
このときの利益はいくらか.
■ 解答 ■
原価を \(1\) とする.
定価は, 原価の \(\color{royalblue}{2}\) 割増 (原価の \(\color{royalblue}{12}\) 割) で
\(1\times\color{royalblue}{1.2}=1.2\)
売値は, 定価の \(\color{magenta}{1}\) 割引 (定価の \(\color{magenta}{9}\) 割) で
\(1.2\color{magenta}{\times 0.9}=1.08\)
利益は, \((売値)-(原価)\) で
\(1.08-1=0.08\)
よって, 求める金額は,
\(1000\ [円]\times0.08=80\ [円]\)
答 \(80\) 円
上の解答は, 原価を \(1\) とした比で利益を表す方法ですが, 比を用いないで計算すると次のようになります.
■ 別解 ■
定価は, 原価の \(\color{royalblue}{2}\) 割増 (原価の \(\color{royalblue}{12}\) 割) で
\(\displaystyle1000\color{royalblue}{\times\frac{12}{10}}\ [円]\)
売値は, 定価の \(\color{magenta}{1}\) 割引 (定価の \(\color{magenta}{9}\) 割) で
\(\displaystyle1000\times\frac{12}{10}\color{magenta}{\times\frac{9}{10}}\)
\(\displaystyle=1000\times\frac{108}{100}\)
\(=1080\ [円]\)
よって,
\(\color{red}{(利益)=(売値)-(原価)}\)
\(=1080-1000\)
\(=80\ [円]\)
答 \(80\) 円
「原価」 の代わりに 「仕入れ値」 とかいてあっても同じ意味です.
ただし, 上の問題からわかるように, 「売値」 は 「定価」 と同じとは限りません.
SPONSORED LINK