おまえのもの は おれのもの
おまえ自身 は おまえのもの
てことは おまえは おれのもの ♡
■命題 って?■
正しい (真) か, 正しくない (偽) かがはっきりと決まる事柄.
「\(p\) ならば \(q\)」 の形で表されるものが多い. 記号では 「\(p \Longrightarrow q\)」 とかく.
そして, この \(p\) とか \(q\) にあたるものを 条件 という.
「\(x\) が \(7\) ならば \(x\) は \(5\) より大きい」 は命題. 真だと判断できるから.
「\(x\) が \(7\) ならば \(x\) は \(5\) より小さい」 も命題. 偽だと判断できるから.
「\(x\) が \(7\) ならば \(x\) は大きい数である」 は命題でない. 真とも偽とも判断できないから.
人の年齢だったら \(7\) 歳は小さいだろうし,
これまでに当たったことのある隕石の個数だったら \(7\) 個は大きい.
■三段論法■
「\(p \Longrightarrow q\)」, 「\(q \Longrightarrow r\)」 がともに真であるとき,
「\(p \Longrightarrow r\)」 も真になる.
例えば, 「人間ならば動物だ」, 「動物ならばいつか死ぬ」 がともに真であることから,
「人間ならばいつか死ぬ」 も真である.
このことは, 集合の図 (ベン図) を書いても納得できるはずだ.
「人間ならば動物だ」 というのは, 「人間の集合が動物の集合に含まれる」 ことと同じ.

「動物ならばいつか死ぬ」 というのは, 「動物の集合がいつか死ぬものの集合に含まれる」 ことと同じ.
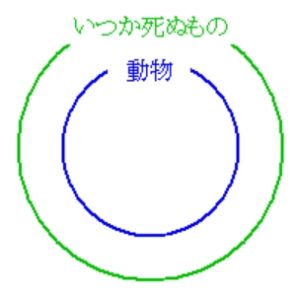
ゆえに, 「人間の集合がいつか死ぬものの集合に含まれる」.
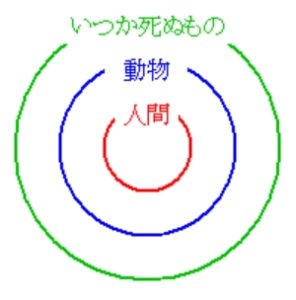
つまり, 「人間ならばいつか死ぬ」.
以上の命題のつなげ方を 三段論法 というが,
いくつでもつなげて四段論法, 五段論法, \(\cdots\) とできる.
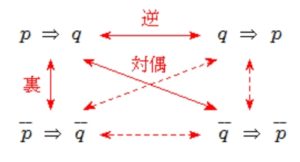
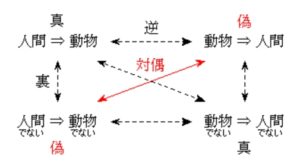
■逆・裏・対偶■
\(p \Longrightarrow q\) \(\cdots\) (A)
という命題に対して,
\(q \Longrightarrow p\)
を (A) の 逆 という.
気をつけたいのは,
逆は, もとの命題と真偽が一致するとは限らない.
ということだ.
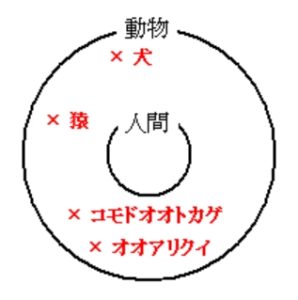
「人間ならば動物だ」 は真だが, その逆 「動物ならば人間だ」 は偽.
犬や猿, オオアリクイやコモドオオトカゲなど, 反例 がいくらだってある.
また, 「\(2x=10\) ならば \(x=5\) である」 は真で,
その逆 「\(x=5\) ならば \(2x=10\) である」 も真.
もとの命題とその逆は, 真偽が一致することもしないこともあるということがわかるね.
条件 \(p\) の 否定 「\(p\) でない」 を \(\color{red}{\overline{p}}\) で表し, 「\(p\) バー」 と読む.
国民的氷菓子 「ス〇カバー」 は \(\overline{ス〇カ}\). たしかにスイカではない.
「あ〇きバー」 や 「チョ〇バー」 に関しては疑問が残るがそんなことはどうでもいい.
命題 (A) に対して,
\(\overline{p} \Longrightarrow \overline{q}\)
を, (A) の 裏 という.
裏も, もとの命題と真偽が一致するとは限らない.
「人間ならば動物だ」 は真だが, その裏 「人間でないならば動物でない」 は偽.
犬や猿, オオアリクイやコモドオオトカゲは人間ではないが動物だ (反例).
命題 (A) の逆の裏, あるいは裏の逆
\(\overline{q}\Longrightarrow\overline{p}\)
を (A) の 対偶 という.
次が重要!
対偶は, もとの命題と真偽が一致する.
「人間ならば動物だ」 は真で, その対偶 「動物でないならば人間でない」 も真.
このことは, 「動物でないものの集合」 が 「人間でないものの集合」 に含まれることからもわかるだろう.
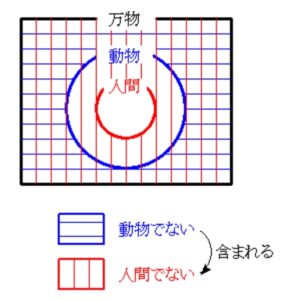
対偶とは, 実は 「言い換え」 をしているにすぎない.
合コンの幹事が, 決定した場所や日時について
「変更があれば連絡します (\(p\Longrightarrow q\))」
と言った場合,
「連絡がなかったら変更がない (\(\overline{q}\Longrightarrow\overline{p}\))」
ということと同じだ.
前日になっても何も連絡がないからといって
「どうなってんすか?」
とか聞く人は論理力が足りない.
ちなみに, 「人間ならば動物だ」 の逆と裏どうしも対偶なので, ともに偽ということで真偽が一致している. 反例までまったく同じだ.
●例題 1 <「ならば」の命題>●
次の命題 (a), (b) が真であるとする.
(a) 数学力があるなら論理力がある.
(b) 文章力がなければ論理力がない.
このとき, 次の命題のうち真といえるものをすべて選べ.
① 数学力があるなら文章力がある.
② 文章力があるなら数学力がある.
③ 数学力がなければ文章力がない.
④ 文章力がなければ数学力がない.
⑤ 精神的に向上心のないものは馬鹿だ.
●解答●
条件 「数学力がある」, 「論理力がある」, 「文章力がある」 をそれぞれ 「\(数\)」, 「\(論\)」, 「\(文\)」 と書くことにする.
(a) \(数\Longrightarrow論\)
(b) \(\overline{文}\Longrightarrow\overline{論}\) (対偶:\(論\Longrightarrow文\))
が真であるとき,
\(数\Longrightarrow論\Longrightarrow文\)
すなわち,
\(数\Longrightarrow文 \cdots\) (A)
も真である.
① \(数\Longrightarrow文\)
これは (A) そのもので, 真といえる.
② \(文\Longrightarrow数\)
これは (A) の逆で, 真とはいえない.
③ \(\overline{数}\Longrightarrow\overline{文}\)
これは (A) の裏で, 真とはいえない.
④ \(\overline{文}\Longrightarrow\overline{数}\)
これは (A) の対偶で, 真といえる.
⑤ 「精神的に向上心がない」, 「馬鹿だ」 という条件は命題 (a), (b) に無関係なので, 真とはいえない.
答 ①, ④
どんなに夏目漱石が好きでも ⑤ を選んではいけません.
これは論理の問題なのであって, 個人的な意見, 経験, 感想を問うものではないのです.
なお, 「数学力」, 「論理力」, 「文章力」 という言葉の意味も, この問題においては考える必要はありません.
SPONSORED LINK
■「存在」の命題■
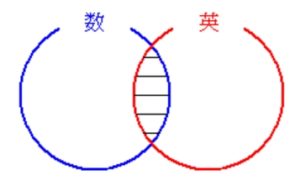
「数学が好きな者の中には英語が好きな者が存在する」
のように, 「\(p\) ならば \(q\)」 の形で表しにくい命題は ベン図 で表すとよいだろう.
数学が好きな者の集合を 「\(\color{blue}{数}\)」,
英語が好きな者の集合を 「\(\color{red}{英}\)」 で表すと,
「\(\color{blue}{数}\)」 と 「\(\color{red}{英}\)」 は共通部分をもつ (一方が他方を包含する場合も含む) ということだ.
●例題 2 <「存在」の命題>●
次の命題 (a), (b) が真であるとする.
(a) 数学が好きな者は国語が好きである.
(b) 数学が好きな者の中には英語が好きな者が存在する.
このとき, 次の命題のうち真といえるものをすべて選べ.
① 国語が好きな者は数学が好きである.
② 英語が好きな者は数学が好きである.
③ 英語が好きな者は国語が好きである.
④ 数学・国語・英語すべて好きな者が存在する.
⑤ お金で買えない価値がある.
●解答●
数学が好きな者の集合を 「\(\color{blue}{数}\)」,
国語が好きな者の集合を 「\(\color{green}{国}\)」,
英語が好きな者の集合を 「\(\color{red}{英}\)」
として, ベン図をかいて考える.
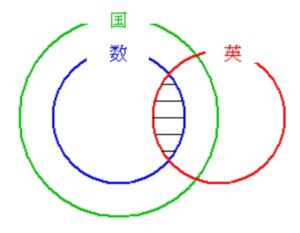
① 「\(\color{green}{国}\)」 に属すが 「\(\color{blue}{数}\)」 に属さない者がいる可能性があるので, 真とはいえない.
② 「\(\color{red}{英}\)」 に属すが 「\(\color{blue}{数}\)」 に属さない者がいる可能性があるので, 真とはいえない.
③ 「\(\color{red}{英}\)」 に属すが 「\(\color{green}{国}\)」 に属さない者がいる可能性があるので, 真とはいえない.
④ 「\(\color{blue}{数}\)」, 「\(\color{green}{国}\)」, 「\(\color{red}{英}\)」 の \(3\) つの集合が共通部分をもつので, 真といえる.
⑤ 「お金で買えない価値がある」 という条件は命題 (a), (b) に無関係なので, 真とはいえない.
答 ④
「偶」=「ペア」
「偶数」 はペアがつくれる数.
「配偶者」 は人生のペア. 運命共同体.
「対偶」 は対角線上のペア. 真偽の運命共同体.