\(5\) % の食塩水と, \(13\) % の食塩水を混ぜると \(5+13=18\) % になるという人に言いたい.
\(5\) ℃ の水と \(13\) ℃の水を混ぜると \(5+13=18\) ℃ になりますか?
だったら世界のエネルギー問題はすべて解決です.
● 加重平均 ●
ある大学が, 入試で英数 \(2\) 科目の得点の平均で合否を決めたいと考えた.
例えば, 英語が \(50\) 点で数学が \(90\) 点だったら, \(2\) 科目の平均をとって,
\(\displaystyle\frac{50+90}{2}=70\) 点
となる.
これを数直線で表現すると, \(70\) 点の位置は \(50\) 点と \(90\) 点の中点にあたる.
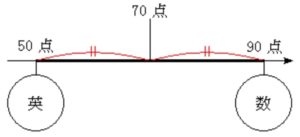
同じ質量の \(2\) つのおもりをつり下げたてんびんが, それらの位置の中点を支点としてつり合うのと似ているね.
しかし理系の学部だったら,
\(英:数=1:3\)
つまり, 英語に対して数学に \(3\) 倍のウエイトをおきたいということがあるだろう.
そういうときは, 「英数数数 \(4\) 科目」 の入試と考えて,
\(\displaystyle\frac{50+90+90+90}{4}=80\) 点
とすればよい. これが 加重平均 とよばれるものだ.
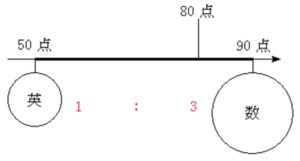
結果, 平均がかなり数学寄りになったのがわかる.
具体的には, この \(80\) 点の位置は, 英語の得点の位置からの距離が
\(80-50=30\)
数学の得点からの距離が
\(90-80=10\)
だから,
\((英語からの距離):(数学からの距離)=3:1\)
そう, 得点のウエイト \(英:数=1:3\) の逆比になっている.
距離の比はウエイトの比の逆比
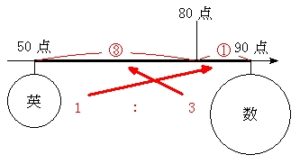
実際, てんびんに質量比 \(1:3\) のおもりをつり下げると, 図のように, つり下げた位置を \(3:1\) に分ける位置を支点としてつり合う.
さて, \(5\) % の食塩水と, \(13\) % の食塩水を同じ量 \(100\) g ずつとって混ぜると, 何 % になるかな?
「しょっぱさ \(5\)」 の食塩水と 「しょっぱさ \(13\)」 の食塩水を同じ量ずつ混ぜるわけだから, ちょうど中間の 「しょっぱさ \(9\)」 になると考えられる.
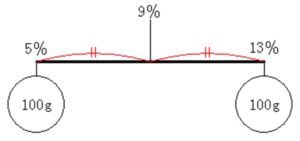
※ 図では数直線の矢印は省略してあります.
では, \(5\) % の食塩水 \(100\) g と, \(13\) % の食塩水 \(300\) g を混ぜると, 何 % になるか. つまり, しょっぱくないほうに対してしょっぱいほうのウエイトが \(3\) 倍の場合だ.
■ 例題 1 <混合後の濃度> ■
\(5\) % の食塩水 \(100\) g と, \(13\) % の食塩水 \(300\) g を混ぜると, 何 % の食塩水になるか.
■ 解答 ■
混合後の濃度を \(x\) % とおく.
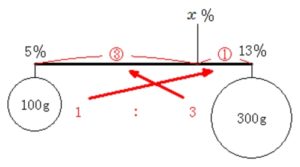
\((x-5):(13-x)=3:1\)
より,
\(x-5=3(13-x)\)
\(x-5=39-3x\)
\(4x=44\)
\(x=11\)
答 \(11\) %
次のように計算してもよいでしょう.
これなら暗算でも答えが出ます.
■ 別解 ■
混合後の濃度を \(x\) % とする.
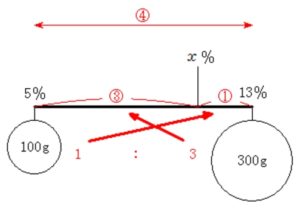
図において,
\(\color{red}{④}=13-5=8\) %
\(\color{red}{①}=8\div4=2\) %
\(\color{red}{③}=2\times3=6\) %
よって,
\(x=5+6=11\) %
答 \(11\) %
Point <濃度算>★★★
てんびん法 (加重平均)
量の逆比は長さの比
逆に, 混合後の濃度から食塩水の量を求めることもできます.
SPONSORED LINK
■ 例題 2 <食塩水の量> ■
\(4\) % の食塩水 \(600\) g に, \(14\) % の食塩水を何 g 加えると, \(8\) % の食塩水になるか.
■ 解答 ■
\(14\) % の食塩水の量を \(x\) g とおく.
\((8-4):(14-8)=4:6=2:3\)

\(600:x=3:2\)
より,
\(3x=1200\)
\(x=400\)
答 \(400\) g
以上の解法が 「てんびん法」 とよばれているものです.
加えるものが 「水」, 「塩」 である場合もそれぞれ 「\(0\) % 食塩水」, 「\(100\) % 食塩水」 と考えることにより, この解法が使えます.
なお, \(3\) 種類の食塩水を混ぜる場合は \(2\) 回に分けて計算を行えば O.K.