
このサイトとかけて
川を上る船と解く
その心は…
■流水算 って?■
往復の際, 行きと帰りで速さが変わる問題.
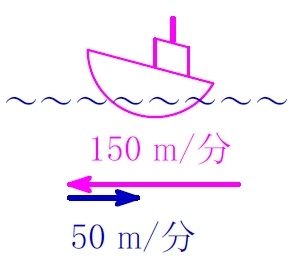
水の流れのないところではつねに分速 \(150\ {\rm m}\) で進む船があるとする.
湖のような水の流れのないところで船などが進む一定の速さを 「静水での速さ」 とよぶことにしよう.
当然, 水の流れのあるところでは, この速さで進むことはない.
いま, 流速 が分速 \(50\ {\rm m}\) である川を考えよう.
この川は, \(1\) 分の間に \(50\ {\rm m}\) だけ船を流れの方向に動かす力をもつ.
静水での速さが分速 \(150\ {\rm m}\) である船がこの川を下る場合,
船が自身の性能により \(1\) 分で \(150\ {\rm m}\) 進んでいる間に,
同じ向きに流れる川が \(50\ {\rm m}\) だけさらに船の背中を押してくれるので,
\(1\) 分で合計 \(\color{magenta}{150}+\color{royalblue}{50}=200\ [{\rm m}]\) 進める.

船は分速 \(200\ {\rm m}\) で川を下ることができるんだ.
\(\bf{\color{red}{(下りの速さ)=(静水での速さ)+(流速)}}\)
逆に, 川を上る場合は,
船が自身の性能により \(1\) 分で \(150\ {\rm m}\) 進んでいる間に,
逆流する川が \(50\ {\rm m}\) だけ船を押し戻してしまう.
結局, \(1\) 分で合計 \(\color{magenta}{150}-\color{royalblue}{50}=100\ [{\rm m}]\) しか進めない.
船は分速 \(100\ {\rm m}\) で川を上ることになる.
\(\bf{\color{red}{(上りの速さ)=(静水での速さ)-(流速)}}\)
流水算では,
下りの速さ, 上りの速さ, 静水での速さ, 流速
という \(4\) 種類の速さが出てくるので, 慣れない人にはパニックだ.
そこで, これらを
数直線に整理
してみよう.
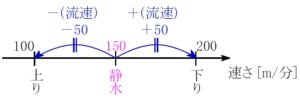
そうすると,
静水での速さは上りと下りの平均 (真ん中)
というのも視力があればわかる.
SPONSORED LINK
●例題 <静水での速さ / 流速>●
ある川の \(20\ {\rm km}\) 離れた \(2\) 地点間を船が往復したところ, 下りは \(1\) 時間, 上りは \(2\) 時間かかった.
次のものを求めよ.
\((1)\) 船の 静水での速さ
\((2)\) 川の 流速
●解答●
\((1)\) 静水での速さを時速 \(\color{magenta}{x}\ {\rm km}\) とする.
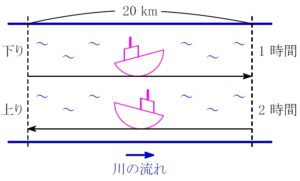
\((下りの速さ)=\displaystyle\frac{20\ [{\rm km}]}{1\ [時間]}=20\ [{\rm km}/時]\)
\((上りの速さ)=\displaystyle\frac{20\ [{\rm km}]}{2\ [時間]}=10\ [{\rm km}/時]\)
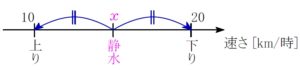
\(\color{magenta}{x}=\displaystyle\frac{10+20}{2}=15\ [{\rm km}/時]\)
答 時速 \(15\ \rm{km}\)
\((2)\)
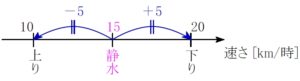
\((\color{royalblue}{流速})=20-\color{magenta}{15}=\color{magenta}{15}-10=5\ [{\rm km}/時]\)
答 時速 \(5\ \rm{km}\)
その心は
下らない.