●例題 1 <順序関係>●
\(\rm P\), \(\rm Q\), \(\rm R\), \(\rm S\), \(\rm T\), \(\rm U\) の \(6\) 人が競走をした結果として, 次の \((\rm a)\) ~ \((\rm f)\) のことがわかっている.
ただし, 同じ順位の者はいない.
\((\rm a)\) \(\rm P\) に勝った者はいなかった.
\((\rm b)\) \(\rm Q\) は \(3\) 位ではなかった.
\((\rm c)\) \(\rm R\) の順位は偶数で, \(\rm S\) より下位だった.
\((\rm d)\) \(\rm S\) の前には \(3\) 人ゴールしていた.
\((\rm e)\) \(\rm T\) は \(\rm S\) より上位だった.
\((\rm f)\) \(\rm U\) の順位は奇数だった.
このとき, 次の問いに答えよ.
\((1)\) 次の イ, ロ, ハ のうち, 確実にいえること をすべて選べ.
イ \(\rm Q\) は \(5\) 位だった.
ロ \(\rm R\) は \(6\) 位だった.
ハ \(\rm T\) は \(\rm U\) より上位だった.
\((2)\) 次の イ, ロ, ハ のうち, 全員の順位を確定させる条件となるもの をすべて選べ.
イ \(\rm T\) が \(2\) 位であること
ロ \(\rm U\) が \(3\) 位であること
ハ \(\rm S\) と \(\rm U\) の順位が連続していること
●解答●
\((\rm a)\) より \(\rm P\) は \(1\) 位.
\((\rm d)\) より \(\rm S\) は \(4\) 位.
\((\rm c)\) より, \(\rm R\) の順位は \(2\) 位か \(4\) 位か \(6\) 位だが, \(\rm S\) より下位なので \(\rm R\) は \(6\) 位.
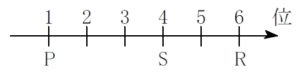
\((\rm e)\) より, \((\hspace{1pt}\rm i\hspace{1pt})\) \(\color{magenta}{\rm T}\) は \(\color{magenta}{2}\) 位 または \((\rm{ii})\) \(\color{magenta}{\rm T}\) は \(\color{magenta}{3}\) 位
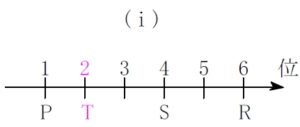
\((\hspace{1pt}\rm i\hspace{1pt})\) の場合
\((\rm b)\) より \(\color{royalblue}{\rm Q}\) は \(\color{royalblue}{5}\) 位.
\((\rm f)\) より \(\color{magenta}{\rm U}\) は \(\color{magenta}{3}\) 位.
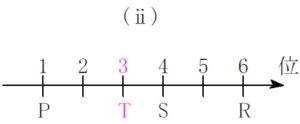
\((\rm ii)\) の場合
\((\rm f)\) より \(\color{royalblue}{\rm U}\) は \(\color{royalblue}{5}\) 位.
\((\rm b)\) より \(\color{magenta}{\rm Q}\) は \(\color{magenta}{2}\) 位.
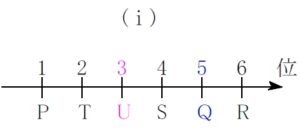

条件 \((\rm a)\) ~ \((\rm f)\) によって, \((\hspace{1pt}\rm i\hspace{1pt})\), \((\rm ii)\) の \(2\) つの可能性が残る.
\((1)\)
イ : \((\rm ii)\) の可能性があるので確実にはいえない.
ロ: \((\hspace{1pt}\rm i\hspace{1pt})\), \((\rm ii)\) より確実にいえる.
ハ: \((\hspace{1pt}\rm i\hspace{1pt})\), \((\rm ii)\) より確実にいえる.
答 ロ, ハ
\((2)\)
イ: \((\rm a)\) ~ \((\rm f)\) にこの条件を加えると,
\((\hspace{1pt}\rm i\hspace{1pt})\) \(\rm{P\ T\ U\ S\ Q\ R}\) で確定.
ロ: \((\rm a)\) ~ \((\rm f)\) にこの条件を加えると,
\((\hspace{1pt}\rm i\hspace{1pt})\) \(\rm{P\ T\ U\ S\ Q\ R}\) で確定.
ハ: \((\hspace{1pt}\rm i\hspace{1pt})\), \((\rm ii)\) ともにこの条件を満たすので, \((\rm a)\) ~ \((\rm f)\) にこの条件を加えても全員の順位は確定しない.
答 イ, ロ
SPONSORED LINK
●例題 2 <位置関係>●
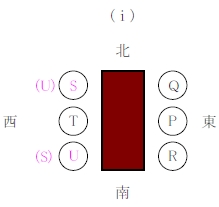
\(\rm P\), \(\rm Q\), \(\rm R\), \(\rm S\), \(\rm T\), \(\rm U\) の \(6\) 人が, テーブルをはさんで東側と西側に \(3\) 人ずつに分かれて向かい合い, 等間隔に着席している.
その位置関係について, 次の \((\rm a)\) ~ \((\rm e)\) のことがわかっている.
\((\rm a)\) \(\rm P\) と \(\rm R\) は隣り合っている.
\((\rm b)\) \(\rm Q\) は北側の端に座っている.
\((\rm c)\) \(\rm S\) と \(\rm U\) は隣り合っていない.
\((\rm d)\) \(\rm Q\) と \(\rm R\) 同じ側に座っている.
\((\rm e)\) \(\rm P\) は東側に座っていて, \(\rm T\) と向かい合っている.
このとき, 次の イ, ロ, ハ のうち, 確実にいえること をすべて選べ.
イ \(\rm S\) は西側の最も南に座っている.
ロ \(\rm T\) は西側の真ん中に座っている.
ハ \(\rm U\) は西側の最も北に座っている.
●解答●
\((\rm a)\), \((\rm d)\) より, \(\rm P\), \(\rm Q\), \(\rm R\) は同じ側に座っている.
\((\rm b)\), \((\rm e)\) より,
\((\hspace{1pt}\rm i\hspace{1pt})\) 東側で北から順に \(\rm Q\), \(\rm P\), \(\rm R\)
または
\((\rm ii)\) 東側で北から順に \(\rm Q\), \(\rm R\), \(\rm P\)
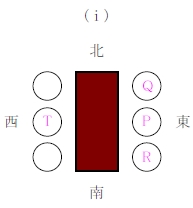
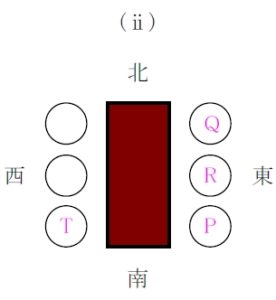
\((\rm ii)\) は \(\rm S\) と \(\rm U\) が隣り合うしかないので, \((\rm c)\) に矛盾.
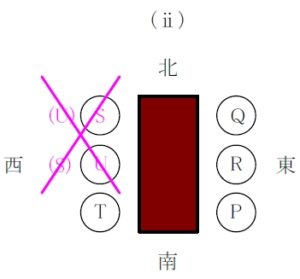
よって, \((\hspace{1pt}\rm i\hspace{1pt})\) の場合に限る.