
■旅人算って?■
複数のものが動いて, 出会ったりすれ違ったり追いついたり追い越したりする速さの問題.
■その前に 速さ って?■
単位時間 (\(1\) 秒, \(1\) 分, \(1\) 時間, \(\cdots\)) あたりに進む距離または道のり.
例えば, 分速 \(100\ {\rm m}\) といえば, \(1\) 分あたり \(100\ {\rm m}\) 進む速さということだ.
\(2\) 分なら \(100\ [{\rm m}/分]\times2\ [分]=200\ [{\rm m}]\) 進む.
\(3\) 分なら \(100\ [{\rm m}/分]\times3\ [分]=300\ [{\rm m}]\) 進む.
\(\cdots\)
こう考えれば, \((速さ)\times(時間)=(距離)\) という式など
公式というより常識
だ. 大事なことは,
覚えるのではなく理解する
こと.
●例題 1 <すれ違い>●
\(2400\ {\rm m}\) 離れた \(2\) 地点から, 分速 \(200\ {\rm m}\) で走る A と, 分速 \(100\ {\rm m}\) で走る B が, 同時に出発して向かい合って走るとき, 出発してから \(2\) 人がすれ違うまでに何分かかるか.
●解答●
求める時間を \(x\) 分とする.
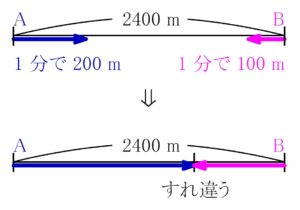
A と B が進んだ距離の和が \(2400\ {\rm m}\) に達したとき, \(2\) 人はすれ違う.
A と B が進む距離の和は
\(1\) 分で \(\color{royalblue}{200}+\color{magenta}{100}=300\ [{\rm m}]\)
\(x\) 分で \(2400\ [{\rm m}]\)
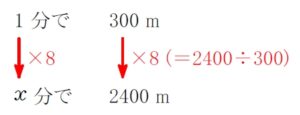
\(x=1\color{red}{\times8}=8\)
答 \(8\) 分
●別解●
求める時間を \(x\) 分とする.
\(({\rm A}\ が進んだ距離)+({\rm B}\ が進んだ距離)=2400\ [{\rm m}]\)
より
\(\color{royalblue}{200}x+\color{magenta}{100}x=2400\)
\(300x=2400\)
\(x=8\)
答 \(8\) 分
SPONSORED LINK
■単位の換算■
\(1\ [時間]=60\ [分]\)
\([時間]\) を \([分]\) に換えると, 数字の部分が \(60\) 倍になるということ.
その他の単位の換算も同じようにできる.
●例題 2 <追いつき>●
\(1\) 周 \(3\ {\rm km}\) の池の周りのある地点から, 時速 \(12\ {\rm km}\) で歩く A と, 時速 \(8\ {\rm km}\) で歩く B が同時に出発して, 池の周に沿って同じ方向に歩くとき, 出発してから A が B に最初に追いつくまでに何分かかるか.
●解答●
求める時間を \(x\) 時間とする.
A と B が進んだ距離の差が \(3\ {\rm km}\) (\(1\) 周) に達したとき, A が B に追いつく.
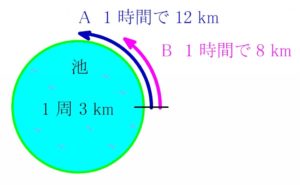
A と B が進む距離の差は,
\(1\) 時間で \(\color{royalblue}{12}-\color{magenta}{8}=4\ [{\rm km}]\)
\(x\) 時間で \(3\ [{\rm km}]\)
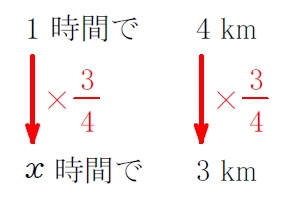
\(x=\displaystyle1\color{red}{\times\frac{3}{4}}=\frac{3}{4}\ [{\rm時間}]=\frac{3}{4}\times60\ [{\rm分}]=45\ [{\rm分}]\)
答 \(45\) 分
●別解●
求める時間を \(x\) 時間とする.
\(({\rm A}\ が進んだ距離)-({\rm B}\ が進んだ距離)=3\ [{\rm km}]\)
より,
\(\color{royalblue}{12}x-\color{magenta}{8}x=3\)
\(4x=3\)
\(x=\displaystyle\frac{3}{4}\ [時間]\)
答 \(45\) 分
恋とは相手に向かって歩み寄ること
愛とは \(2\) 人で同じ方向へ歩むこと
恋愛は旅人算
恋しすぎると, いつかすれ違う
愛は歩幅を合わせないと離れていく