展開図の問題に高い IQ は必要ありません.
■立方体の展開図■
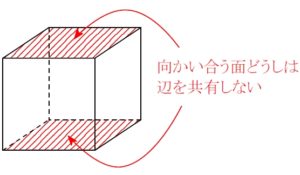
次のような立方体の展開図で, 面 ア と向かい合う面 (平行な面, 対面) はどれ?
脳内で組み立てようとした人, 注意信号だ.
単純な問題ならそれで解けることもあるが, 複雑な問題になると限界がくる.
大事なことは
組み立てたつもりになる
こと.
実は,
組み立てたときにどの辺どうしが重なるかを把握する
ことで, 組み立てたのと同じ効果が得られるんだ.
立方体の展開図について, 辺どうしが重なる際のルールが \(3\) つあるので, それらを紹介しよう.
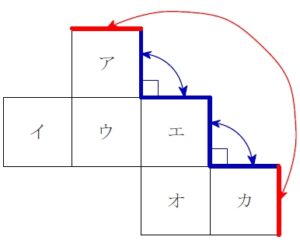
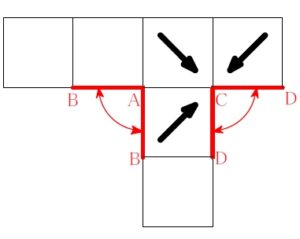
ルール ① 直角をはさむ \(\color{red}{2}\) 辺どうし重なる
展開図の輪郭を見たとき, 直角になっているところは, 組み立てるとそこが閉じて辺どうしが重なる.
この辺の組を 「直角ペア」 とでも名付けようか.
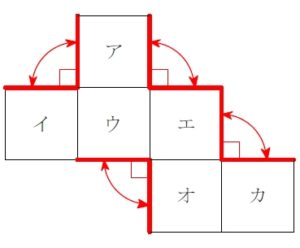
ルール ② その外側どうしも重なる
「直角ペア」 の両サイドについている辺どうしも重なる.
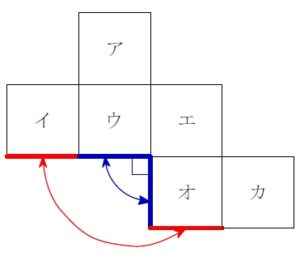
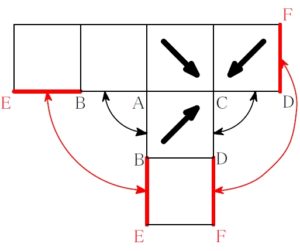
もちろん, さらにその外側どうしも重なる.
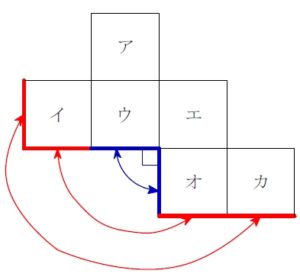
\(2\) つの 「直角ペア」 が隣接する場合は, それでひとかたまりと考える.
「W 直角ペア」 だ. 実際 「W」 みたいな形してるし.
その外側の辺どうしも重なる.
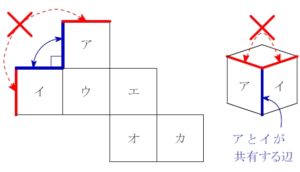
ルール ③ \(\color{red}{2}\) つの面が共有するのはただ \(\color{red}{1}\) 辺
\(2\) つの面が \(2\) 辺以上を共有してしまうような状態は N.G.
ちなみに, 以上の \(3\) つのルールにしたがってもうまく辺の組がつくれない場合, それは組み立てること自体が不可能な展開図だ.
さて, 最初の問いの答えは, 次の例題の解答で示そう.
●例題 1 <立方体の向かい合う面と展開図>●
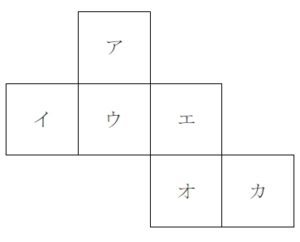
次のような立方体の展開図で, 面 ア と向かい合う面は イ ~ カ のどれか.
●解答●
重なる辺どうしを把握することで, 面 イ, ウ, エ, カ はいずれも面 ア と辺を共有することがわかる.
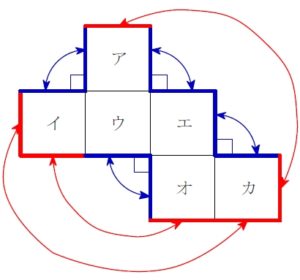
残った面 オ は, 面 ア と辺を共有しないので, 面 ア と向かい合う面である.
答 オ
SPONSORED LINK
次の問題は, 重なる辺だけでなく, 重なる 「頂点」 も把握しなければいけません.
そこで, 重なる辺の組を考えるついでに, 重なる頂点に同じ名前 (アルファベットなど) をつけていきます.
●例題 2 <立方体と展開図の対応>●
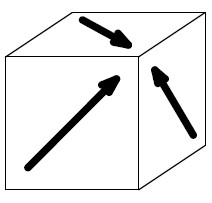
図の立方体の展開図であるものをすべて選べ.
イ
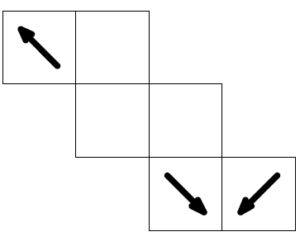
ロ
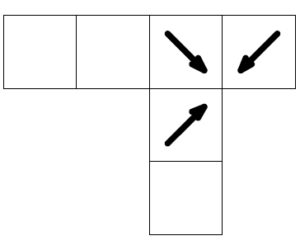
ハ
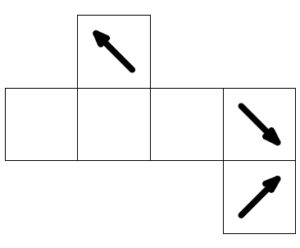
●解答●
この立方体の特徴は, \(3\) つの面に \(1\) つずつ描かれた矢印が同じ \(1\) つの頂点を指していることである.
展開図を組み立てたときに重なる辺の組を把握し, 重なる頂点には同じアルファベットを与えていく.
イ
ルール ① 直角をはさむ \(\color{red}{2}\) 辺どうし重なる
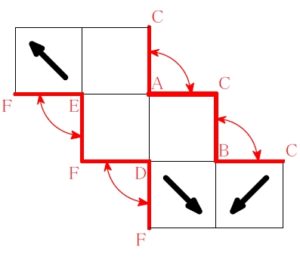
ルール ② その外側どうしも重なる
ルール ③ \(\color{red}{2}\) つの面が共有するのはただ \(\color{red}{1}\) 辺
に反していないことを確認する.
\(3\) つの矢印が同じ \(1\) つの頂点 (\(\rm H\)) を指しているので適する.
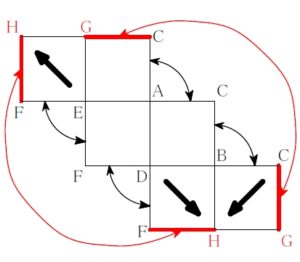
ロ
\(3\) つの矢印が同じ \(1\) つの頂点を指しているが, そもそも 「立方体」 として組み立てられないようでは答えにならない.
ルール ① 直角をはさむ \(\color{red}{2}\) 辺どうし重なる
ルール ② その外側どうしも重なる
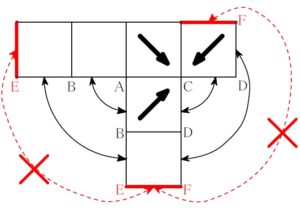
ルール ③ \(\color{red}{2}\) つの面が共有するのはただ \(\color{red}{1}\) 辺
に反しないように辺 \(\rm{EF}\) に重なる辺を探すと, それが存在せず, 不適.
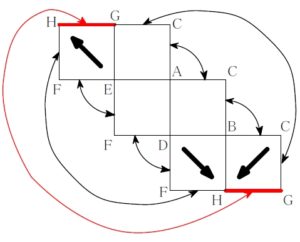
ハ
ルール ① 直角をはさむ \(\color{red}{2}\) 辺どうし重なる

ルール ② その外側どうしも重なる
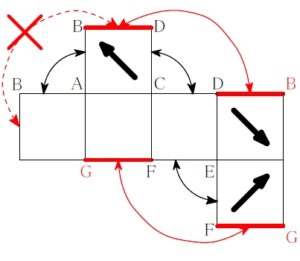
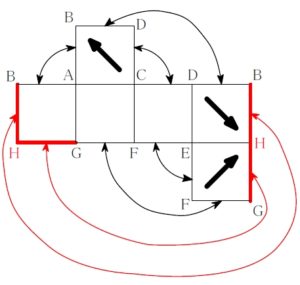
ルール ③ \(\color{red}{2}\) つの面が共有するのはただ \(\color{red}{1}\) 辺
に反していないことを確認する.
\(2\) つの矢印が指す頂点 (\(\rm H\)) と, 残り \(1\) つの矢印が指す頂点 (\(\rm B\)) が異なるので, 不適.
答 イ
解く早さにこだわりすぎると, 上のイロハの ロ のような選択肢にひっかかってしまいがちです.
まさに意外な 「展開」.
とくに, 「〇〇秒で解ける」 的な, 早さ第一主義の解法に飛びついてしまう人は注意が必要です.
いわゆる 「裏技」 的な解法は, しっかりした数学力, というより論理的思考力があってはじめて使いこなせるものです.
そもそも, 裏技が使える問題であることを見抜ける力は, 多くの練習を積まないと培えません.
さらに言うと, 実際の試験で裏技的に解ける問題が出る割合はそれほど多くないと思います.
では, なぜ問題集や参考書で, そういう問題を多く見かけるのか?
答えは簡単です.
その本を執筆した人が, 自分の 解法を説明するのに都合のよい問題を選んで掲載しているからです.
じゃあ, 数学が苦手な人はどうすればよいのか.
この答えも簡単です.
原理原則にしたがった解法を何度も練習し, それを超高速でできるようにすればよいのです.
〇〇秒よりよっぽど早く確実に解けると思います.
満点は取れなくても, 合格点は取れる.
これでいいんです.