
作: E.T.
実際は 「つる」 と 「かめ」 の代わりにいろんなものが出てきます.
某大学の SPI 講座で 「カブトムシ」 を登場させたら, 昆虫の足の本数を忘れて解けない学生がいたとか.
しかし鷹とウサギだったら…
■ 例題 ■ <鶴亀算>
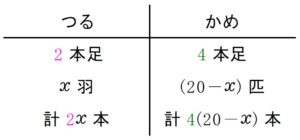
つる と かめ が合わせて \(20\) おり, 足の数の合計が \(70\) 本である.
つる は何羽いるか.
■ 解答 ■ <方程式>
つる は \(\color{magenta}{2}\) 本足, かめ は \(\color{green}{4}\) 本足である.
つる の数を \(x\) 羽とおくと, かめ の数は \((20-x)\) 匹と表される.
\((つる\ の足の総数)+(かめ\ の足の総数)=70\ [本]\)
より,
\(\color{magenta}{2}x+\color{green}{4}(20-x)=70\)
\(\color{magenta}{2}x+\color{green}{4}\times 20-\color{green}{4}x=70\)
\((\color{magenta}{2}-\color{green}{4})x=70-80\)
\(-\color{red}{2}x=-10\)
\(x=10 \div \color{red}{2}\)
\(x=5\)
答 \(5\) 羽
かめ の数を \(y\) 匹とおいてわざわざ \(2\) 文字にする必要はないでしょう.
連立方程式になってすぐさま \(1\) 文字消されちゃうわけですから,
はじめから \(1\) 文字にしとけばよいのです.
SPONSORED LINK
思わず方程式で解いてしまいましたが, 次の別解のように考えてもO.K.
中学受験の経験がある人はこっちで可.
そうでない人は, 見慣れない解法を新しく覚えなきゃいけないので, 原則スルー.
■ 別解 ■ <差集め>
つる が \(0\) 羽 (\(20\) 体すべて かめ) だとすると, 足の数の合計は \(80\) 本 (\(\color{green}{4}\times20=80\)).
しかし, 実際は \(70\) 本で, \(80\) 本よりは \(10\) 本 減っている (\(70-80=-10\)).
つる \(1\) 羽と かめ \(1\) 匹の足の数の差は \(\color{red}{2}\) 本 (\(\color{magenta}{2}-\color{green}{4}=-\color{red}{2}\)) なので,
かめ \(20\) 匹のうちの \(1\) 匹を つる \(1\) 羽に替えると,
足の数の合計は \(\color{red}{2}\) 本だけ減ることになる.
つる を \(1\) 羽にすると \(\color{red}{2}\) 本 減るので,
つる を \(5\) 羽にすると \(10\) 本 減る (\(10 \div \color{red}{2}=5\)).
答 \(5\) 羽
どちらの解法も, 実は同じ計算をしているのがわかりますね!
Point <鶴亀算>★★★
\([1]\) 求めるものを \(x\) とおいて方程式
\([2]\) 求めるものがいない (\(0\) 匹) とする
鷹とウサギだったら
食物連鎖でウサギ全滅!