
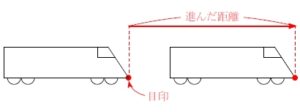
■通過算 って?■
走るもの自身の長さを考慮に入れなければならない速さの問題.
電車など, その長さが無視できないものが出てきたら, 走った距離の測り方に注意!
先頭に 「目印」 をつけて,
その目印がどれだけ進んだかを読み取る.
●例題 1 <通過時間>●
秒速 \(15{\rm m}\) で走る, 長さ \(75{\rm m}\) の電車が線路上の \(1\) 点を通過するのに何秒かかるか.
●解答●
求める時間を \(x\) 秒とする.
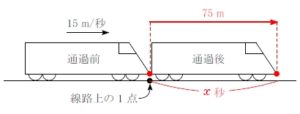
線路上の \(1\) 点を通過する間に電車は自身の長さである \(75{\rm m}\) だけ進むから,
\(x=\displaystyle\frac{75\ [{\rm m}]}{15\ [{\rm m}/秒]}=5\ [秒]\)
答 \(5\) 秒
SPONSORED LINK
■単位の換算■
\(60\ [秒]=1\ [分]\)
なのは有名.
この式からわかるのは, \([秒]\) を \([分]\) に換えると, 数字の部分が \(\displaystyle\frac{1}{60}\) になるということ.
その他の単位の換算も同じようにできる.
●例題 2 <物体の長さ>●
分速 \(1200{\rm m}\) で走る電車が, 長さ \(450{\rm m}\) の橋を渡り始めてから渡り終えるまでに \(30\) 秒かかるとき, この電車の長さは何 \({\rm m}\) か.
●解答●
速さの単位に合わせて, 時間の単位を \([分]\) に直す.
\(30\ [秒]=\displaystyle\frac{30}{60}\ [分]=\frac{1}{2}\ [分]\)
電車の長さを \(x\ [{\rm m}]\) とおく.
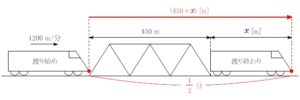
橋を渡り始めてから渡り終えるまでに, 電車は橋の長さと自身の
長さを合わせた\((450+x)\ [{\rm m}]\) 進むから,
\((距離)=(速さ)\times(時間)\)
より,
\(450+x=1200\times\displaystyle\frac{1}{2}\)
\(450+x=600\)
\(x=150\)
答 \(150\ \rm{m}\)
橋を渡り終えた状態とは, 電車の車体が完全に橋から出た状態です.
もし渡り終えていれば, このあと大地震で橋が崩れ去っても電車は平気なはずです.
車体がまだ一部でも橋に乗っていたら平気じゃないですよね. それは渡り終えたとは言いません.