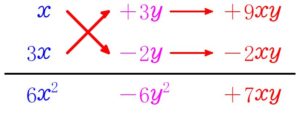
いわゆる 「たすきがけ」 の仕組みを解説します.
● 共通因数のくくり出し ●
\(200\) 円と \(300\) 円で \(500\) 円.
この計算はみんな無意識に \(2+3=5\) を \(100\) 倍しているはずだ.
その一瞬の計算をわざわざ数学的に解説するとこうなる.
\(200+300\)
\(=\color{red}{100}\cdot2+\color{red}{100}\cdot3\)
\(=\color{red}{100}\cdot(2+3)\)
\(=\color{red}{100}\cdot5\)
\(=500\)
\(\color{red}{100}\) を 括弧 \((\ \ \ )\) の前にくくり出しているわけだが,
この \(\color{red}{100}\) は \(200\ (=\color{red}{100}\cdot2)\) と \(300\ (=\color{red}{100}\cdot3)\) に共通に含まれている約数だね.
約数の別名は 「因数」.
\(\color{red}{100}\) は, \(200\) と \(300\) の \(\large\bf\color{blue}{共通因数}\) (\(\rm{common\ factor}\)) だ.
一般化すると,
\(\large\color{blue}{ma+mb=m(a+b)}\)
これが 「共通因数 \(m\) でくくり出す」 ということだ.
分配法則で括弧をはずす計算の逆ね.
いくつか例を挙げておこう.
例 \(1\)
\(10x^3 y^2 -15x^2 y^3\)
\(=\color{red}{5x^2 y^2} \cdot 2x -\color{red}{5x^2y^2} \cdot 3y\)
\(=\color{red}{5x^2 y^2}(2x-3y)\)
(共通因数 \(\color{red}{5x^2 y^2}\) をくくり出した.)
例 \(2\)
\(\color{red}{(x+1)}y+\color{red}{(x+1)}z\)
\(=\color{red}{(x+1)}(y+z)\)
(共通因数 \(\color{red}{x+1}\) をくくり出した.)
このように, 展開する前の状態に戻すのが \(\large\bf\color{blue}{因数分解}\) (\(\rm{factorization}\)) .
「因数分解せよ.」 と言われたら, まず
くくり出せる共通因数がないかを必ず確認
しよう.
● 乗法公式の確認 ●
乗法公式
\([1]\) \(\large\color{blue}{x^2 + (a+b)x + ab}\) \(\large\color{blue}{=(x+a)(x+b)}\)
\([2]\) \(\large\color{blue}{a^2 + 2ab + b^2 = (a+b)^2}\)
\([3]\) \(\large\color{blue}{a^2 – 2ab + b^2 = (a-b)^2}\)
\([4]\) \(\large\color{blue}{a^2 – b^2 = (a+b)(a-b)}\)
においては, 右辺から左辺への変形が展開で, 左辺から右辺への変形が因数分解だ.
まず共通因数を確認したら, 次は当てはまる乗法公式がないかを考えよう.
例
\(4x^2 -36y^2\)
\(=4(x^2 -9y^2)\)
(共通因数 \(4\) をくくり出した.)
\(=4\{x^2 -(3y)^2\}\)
\(=4(x+3y)(x-3y)\)
(\(\color{red}{a^2 -b^2=(a+b)(a-b)}\) で \(\color{red}{a}=x\), \(\color{red}{b}=3y\).)
● たすき掛け ●
では, 新しい乗法公式 (因数分解公式)
\(\large\color{blue}{acx^2 +(ad+bc)x+bd}\) \(\large\color{blue}{=(ax+b)(cx+d)}\)
について説明しよう.
実はこれ, 公式として暗記する必要はまったくないんだよ.
「展開の逆算」 を式として表現しただけなんだ.
具体例で説明しよう.
\((\color{blue}{2x}\color{magenta}{+3})(\color{blue}{3x}\color{magenta}{+1})\) \(\cdots\) ①
を分配法則で展開すると,
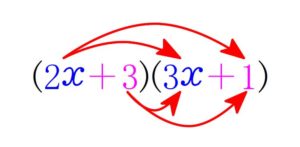
\((\color{blue}{2x}\color{magenta}{+3})(\color{blue}{3x}\color{magenta}{+1})\)
\(=\color{blue}{2x\cdot3x} \color{blue}{+2x}\cdot\color{magenta}{1}\color{blue}{+3x}\cdot\color{magenta}{3}\color{magenta}{+3}\cdot\color{magenta}{1}\)
\(=\color{blue}{6x^2} \color{red}{+2x+9x} \color{magenta}{+3}\)
\(=\color{blue}{6x^2} \color{red}{+11x} \color{magenta}{+3}\) \(\cdots\) ②
ここで, \(1\) 次の項 「\(\color{red}{+11x}\)」 は, もとの式の
「内側」 どうし, 「外側」 どうしを掛けてできる項をまとめたもの
になっていることを覚えておこう.
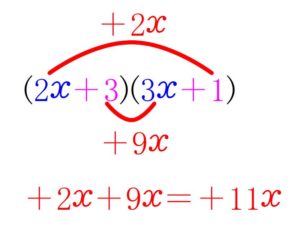
さて, 今度は逆に ② を因数分解してもとの式に戻してみよう.
展開すると ①: \(\color{blue}{6x^2} \color{red}{+11x} \color{magenta}{+3}\) になるような式を逆算するんだ.
まず,
くくり出せる共通因数がないことを確認!
これ大事.
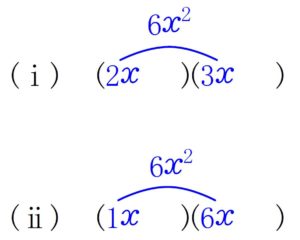
次に, ② の \(2\) 次の項 「\(\color{blue}{6x^2}\)」 に着目しよう. 展開したときにこれが出るとすれば,
\((\rm{i})\) \(\color{blue}{6x^2 =2x\cdot 3x}\) と考えて
\((\color{blue}{2x}\ \ \ \ \ \ \ )(\color{blue}{3x}\ \ \ \ \ \ \ )\)
または
\((\rm{ii})\) \(\color{blue}{6x^2=1x\cdot 6x}\) と考えて
\(\)\((\color{blue}{1x}\ \ \ \ \ \ \ )(\color{blue}{6x}\ \ \ \ \ \ \ )\)
というのがもとの形と考えられるね.
まずは \((\rm{i})\) のほうを採用してみよう.
② の定数項 「\(\color{magenta}{+3}\)」 に着目.
\((\color{blue}{2x}\color{magenta}{\underline{\ \ \ \ \ \ \ }})(\color{blue}{3x}\color{magenta}{\underline{\ \ \ \ \ \ \ }})\)
の \(\color{magenta}{\underline{\ \ \ \ \ \ \ }}\) には積が \(\color{magenta}{+3}\) となるような \(2\) つの数が入るはずだ.
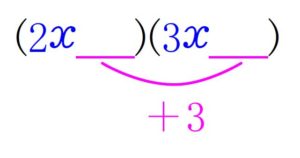
すると, \(\color{magenta}{3=+1\cdot (+3)}\) または \(\color{magenta}{-1\cdot (-3)}\) と考えて
(ア) \((\color{blue}{2x}\color{magenta}{+1})(\color{blue}{3x}\color{magenta}{+3})\)
(イ) \((\color{blue}{2x}\color{magenta}{+3})(\color{blue}{3x}\color{magenta}{+1})\)
(ウ) \((\color{blue}{2x}\color{magenta}{-1})(\color{blue}{3x}\color{magenta}{-3})\)
(エ) \((\color{blue}{2x}\color{magenta}{-3})(\color{blue}{3x}\color{magenta}{-1})\)
の \(4\) つが考えられる.
でも, おかしいのが紛れ込んでるぞ!
(ア) \((2x+1)(\color{red}{3x+3})\)
(ウ) \((2x-1)(\color{red}{3x-3})\)
は, 後ろの \((\ \ \ )\) 内の共通因数 \(\color{red}{3}\) をくくり出せる.
これはもとの式 ② において
くくり出せる共通因数がないことに矛盾する.
だから
(イ) \((\color{blue}{2x}\color{magenta}{+3})(\color{blue}{3x}\color{magenta}{+1})\)
(エ) \((\color{blue}{2x}\color{magenta}{-3})(\color{blue}{3x}\color{magenta}{-1})\)
に絞られる.
最後に, ② の \(1\) 次の項 「\(\color{red}{+11x}\)」 に着目.
先に述べたように, これは
「内側」 どうし, 「外側」 どうしを掛けてできる項をまとめたもの
なので, そうなっているかを調べよう.
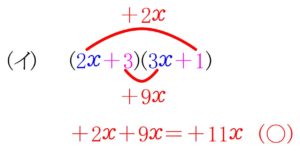
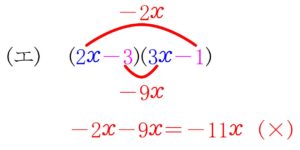
(イ) は O.K. だけど, (エ) は N.G. だね.
よって,
\(\color{blue}{6x^2}\color{red}{+11x}\color{magenta}{+3}=(\color{blue}{2x}\color{magenta}{+3})(\color{blue}{3x}\color{magenta}{+1})\)
となる.
今のようにうまくいかなかったら,
\((\rm{ii})\) \((\color{blue}{1x}\ \ \ \ \ \ \ )(\color{blue}{6x}\ \ \ \ \ \ \ )\)
のほうに切り替えてやってみよう.
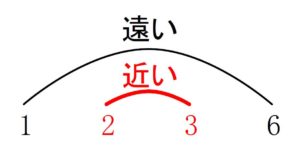
ちなみに, 統計的には
\(1x\) と \(6x\) のような 「遠い数」 の組を含む \(\rm(ii)\) よりも,
\(\color{red}{2}x\) と \(\color{red}{3}x\) のような 「近い数」 の組を含む \(\rm(i)\) のほうが
正解となることが多いぞ.
そして, 実は
\(\large\color{blue}{acx^2 +(ad+bc)x+bd}\) \(\large\color{red}{=(ax+b)(cx+d)}\)
という式で
\(a=2\), \(b=3\), \(c=3\), \(d=1\)
とすれば
\(6x^2 +11x+3=(2x+3)(3x+1)\)
になるんだけど, この 「公式」 に当てはめて因数分解しているという気はさらさらない.
そう, 式を覚えるのではなく, 方法を理解する んだ!
「展開の逆算」 をしているという気持ちがあれば充分.
また, 上で述べた
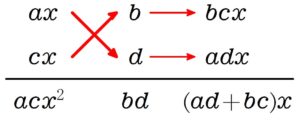
「内側」 どうし, 「外側」 どうしを掛ける
シーンは, \(2\) つの \((\ \ \ )\) 内の式を縦に並べて書くと, 「クロスさせて掛ける」 状態になるため, 「\(\large\bf\color{blue}{たすき掛け}\)」 とよばれることがあるよ.

Point <たすき掛け> ★★
\(\large\color{blue}{acx^2 +(ad+bc)x+bd}\) \(\large\color{blue}{=(ax+b)(cx+d)}\)
「展開の逆算」 で考える.
\(1\) 次の項は 「内側」 どうし 「外側」 どうしを掛けてまとめたもの.
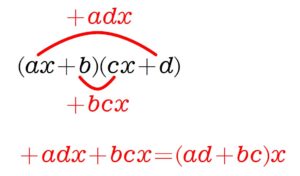
「近い数」 の組から試す.
共通因数がくくり出せる式は却下.
■ 例題 ■ <因数分解 (2次式)>
次の式を因数分解せよ.
\((1)\) \(\color{blue}{6x^2}\color{red}{-x}\color{magenta}{-12}\)
\((2)\) \(\color{blue}{6a^2}\color{red}{+ab}\color{magenta}{-15b^2}\)
\((2)\) 大同工業大 (工)
SPONSORED LINK
■ 解答 ■
\((1)\)
\(\color{blue}{6x^2=2x\cdot 3x}\)
\(\color{magenta}{-12=-3\cdot (+4)}\)
と考えて \((\color{blue}{2x}\color{magenta}{-3})(\color{blue}{3x}\color{magenta}{+4})\) を展開すると,
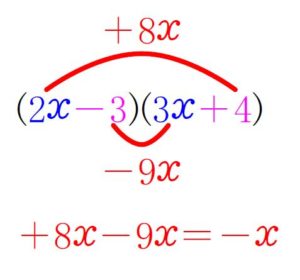
\(\color{red}{-x}\) が出るので,
\(\color{blue}{6x^2}\color{red}{-x}\color{magenta}{-12}=(\color{blue}{2x}\color{magenta}{-3})(\color{blue}{3x}\color{magenta}{+4})\) \(\cdots\) (答)
\((2)\)
\(\color{blue}{6a^2=2a\cdot 3a}\)
\(\color{magenta}{-15b^2=-3b\cdot (+5b)}\)
と考えて \((\color{blue}{2a}\color{magenta}{-3b})(\color{blue}{3a}\color{magenta}{+5b})\) を展開すると,
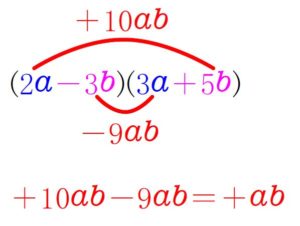
\(\color{red}{+ab}\) が出るので,
\(\color{blue}{6a^2}\color{red}{+ab}\color{magenta}{-15b^2}=(\color{blue}{2a}\color{magenta}{-3b})(\color{blue}{3a}\color{magenta}{+5b})\) \(\cdots\) (答)
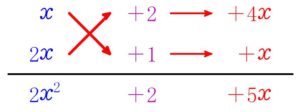
なお, 「たすき掛け」 の形式でかくと次のようになります.
\((1)\)
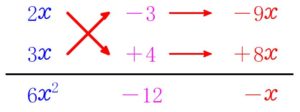
\((2)\)

さあ, 慣れてきたら 「内側どうし, 外側どうし掛けてまとめる」 操作を脳内でやってみましょう.
答案には因数分解の結果だけを書くので充分です.
■ 練習 ■ <因数分解 (2次式)>
次の式を因数分解せよ.
\((1)\) \(\color{blue}{2x^2}\color{red}{+5x}\color{magenta}{+2}\)
\((2)\) \(\color{blue}{6x^2}\color{red}{+17x}\color{magenta}{-143}\)
\((3)\) \(\color{blue}{3x^2}\color{red}{+7xy}\color{magenta}{-6y^2}\)
\((2)\) 東京工科大 (メディア・デザイン 他)
\((3)\) 北海道医療大 (歯・薬)
※ \(143\) を素因数分解すると \(11\cdot 13\) です.
SPONSORED LINK
■ 解答 ■
\((1)\)
\(\color{blue}{2x^2=x\cdot 2x}\)
\(\color{magenta}{2=+2\cdot (+1)}\)
と考えて\((\color{blue}{x}\color{magenta}{+2})(\color{blue}{2x}\color{magenta}{+1})\) を展開すると,
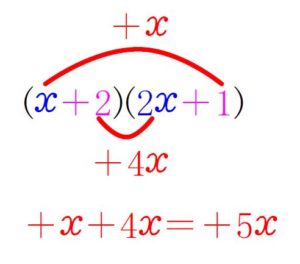
\(\color{red}{+5x}\) が出るので,
\(\color{blue}{2x^2}\color{red}{+5x}\color{magenta}{+2}=(\color{blue}{x}\color{magenta}{+2})(\color{blue}{2x}\color{magenta}{+1})\) \(\cdots\) (答)
\((2)\)
\(\color{blue}{6x^2=2x\cdot 3x}\)
\(\color{magenta}{-143=+13\cdot (-11)}\)
と考えて \((\color{blue}{2x}\color{magenta}{+13})(\color{blue}{3x}\color{magenta}{-11})\) を展開すると,
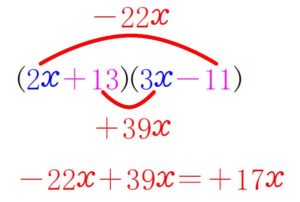
\(\color{red}{+17x}\) が出るので,
\(\color{blue}{6x^2}\color{red}{+17x}\color{magenta}{-143}=(\color{blue}{2x}\color{magenta}{+13})(\color{blue}{3x}\color{magenta}{-11})\) \(\cdots\) (答)
\((3)\)
\(\color{blue}{3x^2=x\cdot 3x}\)
\(\color{magenta}{-6y^2=+3y\cdot (-2y)}\)
と考えて \((\color{blue}{x}\color{magenta}{+3y})(\color{blue}{3x}\color{magenta}{-2y})\) を展開すると,
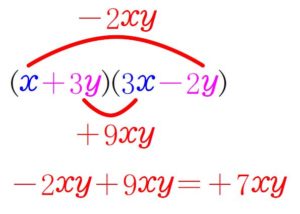
\(\color{red}{+7xy}\) が出るので,
\(\color{blue}{3x^2}\color{red}{+7xy}\color{magenta}{-6y^2}=(\color{blue}{x}\color{magenta}{+3y})(\color{blue}{3x}\color{magenta}{-2y})\) \(\cdots\) (答)
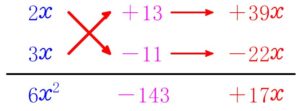
「たすき掛け」 の形式でかくと次のようになります.
\((1)\)
\((2)\)
\((3)\)