1文字整理による因数分解のしかたを解説します.
整式についての解説は 「展開 (1)」 のページを参照してください.
● 降べきの順って? ●
では, 質問.
整式
\(x^2 + 3a^2 x – 5a^3\)
は何次式でしょう?
先頭に \(x^2\) があるから \(2\) 次式?
それは完全な正解ではない.
この整式は
\(x^2\), \(3a^2 x\), \(-5a^3\)
という \(3\) つの 項 から成っているよね.
まず, これらの 項の次数 を見抜く.
掛けられている文字の個数 (「次数は字数」) だ.
係数 (数字の部分) は関係ない.
\(x^2 = \color{red}{x} \cdot \color{red}{x}\) は \(\color{red}{2}\) 次 の項.
\(3a^2 x = 3 \cdot \color{red}{a} \cdot \color{red}{a} \cdot \color{red}{x}\) は \(\color{red}{3}\) 次 の項.
\(-5a^3 = -5 \cdot \color{red}{a} \cdot \color{red}{a} \cdot \color{red}{a}\) も \(\color{red}{3}\) 次 の項.
このうち 最高次の項は \(\color{red}{3}\) 次.
整式の次数とは最高次の項の次数だから,
\(x\) と \(a\) の整式 \(x^2 + 3a^2 x – 5a^3\) は \(\color{red}{3}\) 次式 だ.
話はここで終わらない.
文字 \(\color{red}{x}\) に着目 して \(a\) を数字扱いすると,
\(\color{red}{x^2} + 3a^2 \color{red}{x} – 5a^3\)
は \(\color{red}{x}\) の \(\color{red}{2}\) 次式.
逆に, 文字 \(\color{red}{a}\) に着目 して \(x\) を数字扱いすると,
\(x^2 + 3x \color{red}{a^2} – 5 \color{red}{a^3}\)
は \(\color{red}{a}\) の \(\color{red}{3}\) 次式.
このように, どの文字に着目するかで整式の次数は異なってくる.
ところで, \(\color{red}{x}\) について整理 された
\(\color{red}{x^2} + 3a^2 \color{red}{x} – 5a^3\)
は右の項ほど \(\color{red}{x}\) の次数が下がっているね.
このような項の並び方を \(\large\bf\color{blue}{降べきの順}\) (\(\rm{descending\ order\ of\ powers}\)) という.
「べき」 とは漢字で書くと 「\(\large\bf\color{blue}{冪}\)」 (\(\rm{power}\)) で, 累乗のことだよ.
ちなみに, \(x\) がついていない \(-5a^3\) は \(0\) 次で, 定数項というぞ.
また, \(\color{red}{a}\) について整理 された
\(x^2 + 3x \color{red}{a^2} – 5 \color{red}{a^3}\)
は右の項ほど \(\color{red}{a}\) の次数が上がっているね.
このような項の並び方を \(\large\bf\color{blue}{昇べきの順}\) (\(\rm{ascending\ order\ of\ powers}\)) という.
● 1人を主役に ●
日曜 夜の某国民的シーフード系アニメ 『サ〇エさん』.

毎回 終わりに 「さーて, 来週の〇ザ〇さんは…」
とか言いながら次回のテーマが発表される.

多くのキャラクター (\(\rm{character}\)) が出てくるが,
各テーマは だいたい 「\(\color{red}{1}\) 人が主役」 だ.

因数分解に話を戻そう.
例えば
\(a(b^2 – c^2) + b(c^2 – a^2) + c(a^2 – b^2)\)
みたいに文字がたくさん出てくる式.
「文字」 も英語で \(\rm{character}\).
多くのキャラクターが出てきたら, \(\color{red}{1}\) 人を主役に.
ということで, \(\color{red}{1}\) 文字 \(\color{red}{a}\) に着目 して降べきの順に整理してみよう.
まず \(\color{red}{a}\) に着目.
\(\color{red}{a}(b^2 – c^2) + b(c^2 – \color{red}{a^2}) + c(\color{red}{a^2} – b^2)\)
\(\color{red}{a^2}\) が \(2\) 箇所に分散しているので,
部分的に展開して
\(\color{red}{a}(b^2 – c^2) + bc^2 – b \color{red}{a^2} + c \color{red}{a^2} – b^2 c\)
\(-b \color{red}{a^2}\) と \(+c \color{red}{a^2}\) は 同類項 として扱われるので \(1\) つにまとめる.
\(-(b-c) \color{red}{a^2} + (b^2 – c^2)\color{red}{a} -b^2 c + bc^2\)
\(\color{red}{a}\) を主役にして整理したことによって,
共通因数が見えてくるぞ.
係数部分を因数分解して,
\(-\color{blue}{(b-c)} \color{red}{a^2} + (b+c) \color{blue}{(b-c)} \color{red}{a} – bc \color{blue}{(b-c)}\)
共通因数 \(\color{blue}{b-c}\) をくくり出そう.
\(\color{blue}{(b-c)} \{- \color{red}{a^2} + (b+c) \color{red}{a} – bc\}\)
\(\{\ \ \ \ \ \}\) 内のはじめがマイナス (\(-\)) なのが気持ち悪いので,
\(-1\) もくくり出す (\(\{\ \ \ \ \ \}\) 内を逆符号にする).
\(-(b-c)\{\color{red}{a^2} – (b+c) \color{red}{a} + bc\}\)
あとは
\(\color{red}{a^2} – (2+3)\color{red}{a} + 2 \cdot 3\)
\(=(\color{red}{a} – 2)(\color{red}{a} – 3)\)
みたいに
\(\color{red}{a^2} – (b+c)\color{red}{a} + bc\)
\(=(\color{red}{a} – b)(\color{red}{a} – c)\)
と因数分解できるので, 結果,
\(-(b-c)(\color{red}{a} – b)(\color{red}{a} – c)\)
ここで終わってもいいんだけど,
\(a-c=-(c-a)\) として
\(-(b-c)(a-b)\{-(c-a)\}\)
\((-) \times (-) = (+)\) としてから掛け算の順序変更をして
\(=(a-b)(b-c)(c-a)\)
とすると見栄えがいい.
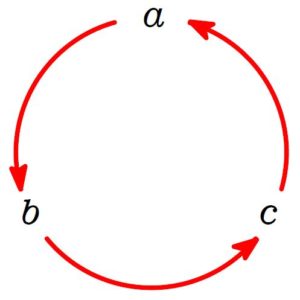
\(a \rightarrow b \rightarrow c \rightarrow a \cdots\)
と文字が循環して式中に現れる書き方を \(\large\bf\color{blue}{輪環の順}\) (\(\rm{cyclic\ order}\)) という.
● 低次の文字に着目 ●
ところで, \(2\) 文字の式
\(x^2 + xy – x – y\)
を \(1\) 文字について整理して因数分解するとしたら,
どっちの文字に着目するといいかな?
おすすめは, 次数の低いほうの文字 だ.
\(x^2 + xy – x – y\)
は, \(x\) に着目すると \(2\) 次式, \(y\) に着目すると \(1\) 次式.
そして, 一般に 次数が低い式のほうが因数分解しやすい はずだ.
\(\color{red}{y}\) について整理すると
\((x-1)\color{red}{y} + x^2 -x\)
定数項の部分を因数分解すると共通因数がでてきて こんにちは.
\(\color{blue}{(x-1)} \color{red}{y} + x \color{blue}{(x-1)}\)
\(\color{blue}{(x-1)}\) をくくり出せば因数分解完了だ.
\(\color{blue}{(x-1)} (\color{red}{y} + x)\)
● 係数が単純な文字に着目 ●
例えば
\(3x^2 + 5xy – 2y^2 – x + 5y -2\)
の因数分解.
\(1\) 文字整理で解くとしたら, \(x\), \(y\) のどっちに着目しようか.
どっちに着目しても \(2\) 次式なので どっちでもいいんだけど,
こういうときは \(\color{red}{2}\) 次の項の係数が単純なほう が おすすめ.
\(x^2\) の係数は \(3\), \(y^2\) の係数は \(-2\) で,
マイナスがつかないほうが単純だよね.
そこで \(\color{red}{x}\) に着目 して整理し, 因数分解してみよう.
\(3 \color{red}{x^2} + 5 \color{red}{x} y – 2y^2 – \color{red}{x} + 5y -2\)
\(5y \color{red}{x}\) と \(- \color{red}{x}\) は同類項としてまとめる.
\(3 \color{red}{x^2} + (5y-1) \color{red}{x} – (2y^2 – 5y + 2)\)
これで \(\color{red}{x}\) の \(2\) 次式として整理したことになる.
ここで
\(3 \color{red}{x^2} + 7 \color{red}{x} – 6 = (3 \color{red}{x} – 2)(\color{red}{x} + 3)\)
のような因数分解を思い出そう.
(参照: 「因数分解 (1)」)
定数項 \(-6\) を \(-2 \cdot 3\) と分解しているのがわかるね.
これと同じように, さっきの式の定数項 \(2y^2 – 5y + 2\) も
\((2y-1)(y-2)\) と分解しておく.
\(3 \color{red}{x^2} + (5y-1) \color{red}{x} – (2y-1)(y-2)\)
そして, 展開すると この式になるものを逆算だ.

ちなみに, いわゆる 「たすき掛け」 の形式で書くと こうだ.

したがって, 与式は
\(\{3 \color{red}{x} – (y-2)\}\{\color{red}{x} + (2y-1)\}\)
\(\color{red}{x}\) を特別扱いせずに書くと
\((3x-y+2)(x+2y-1)\)
これで できあがり.
● 因数分解の手順を確認しよう ●
(参考: 「因数分解 (4)」)
因数分解は
① \(\large\bf\color{blue}{共通因数}\) があればくくり出し,
② 当てはまる \(\large\bf\color{blue}{乗法公式}\) があれば適用する.
③ それでもダメなら次の \(3\) つ.
\(\large\bf\color{blue}{置換}\) \(\cdots\) 式の一部を \(1\) 文字に置き換える.
\(\large\bf\color{blue}{整理}\) \(\cdots\) \(1\) 文字についての式とみて他の文字を係数扱いし, 同類項をまとめる.
\(\large\bf\color{blue}{完成}\) \(\cdots\) 平方完成して \((\ \ \ )^2 – (\ \ \ )^2\) の形をつくる. または, 立方完成して \((\ \ \ )^3 \pm (\ \ \ )^3\) の形をつくる.
いずれかを実行したら ① へ戻る.
今回は 「\(\large\bf\color{blue}{整理}\)」 をマスターしよう.
「\(\large\bf\color{blue}{置換}\)」, 「\(\large\bf\color{blue}{完成}\)」 は別ページで解説するよ.
なお, 前出の
\(x^2 + xy – x – y\)
の因数分解は, はじめから \(\large\bf\color{blue}{共通因数}\) をつくって くくり出してもできるぞ.
\(x^2 + xy – x – y\)
\(=x \color{red}{(x+y)} – 1 \color{red}{(x+y)}\)
\(=\color{red}{(x+y)} (x-1)\)
Point <因数分解の手順> ★★★
① \(\large\bf\color{blue}{共通因数}\) (なければつくれ)
➁ \(\large\bf\color{blue}{公式}\)・\(\large\bf\color{blue}{定理}\)(※)
③ \(\large\bf\color{blue}{置換}\)・\(\large\bf\color{blue}{整理}\)・\(\large\bf\color{blue}{完成}\)
(→ ① へ戻る)
原則, 有理数範囲で限界まで.
※ 別ページで解説する 「因数定理」 を指します.
■ 例題 ■ <複雑な式の因数分解>
次の式を因数分解せよ.
\((1)\) \(x^2 + xy – x – y\)
\((2)\) \(3x^2 + 5xy – 2y^2 – x + 5y -2\)
\((3)\) \(a(b^2 – c^2) + b(c^2 – a^2) + c(a^2 – b^2)\)
\((1)\) 専修大 (ネットワーク情報)
\((2)\) 京都産業大
\((3)\) 龍谷大
SPONSORED LINK
■ 解答 ■
\((1)\)
\(x^2 + x \color{red}{y} – x – \color{red}{y}\)
\(=(x-1)\color{red}{y} + x^2 -x\)
(\(\color{red}{y}\) の \(1\) 次式として整理した.)
\(=\color{blue}{(x-1)} \color{red}{y} + x \color{blue}{(x-1)}\)
\(=\color{blue}{(x-1)} (\color{red}{y} +x)\)
(共通因数 \(\color{blue}{x-1}\) をくくり出した.)
\(=(x-1)(x+y)\) \(\cdots\) (答)
\((2)\)
\(3 \color{red}{x^2} + 5 \color{red}{x} y – 2y^2 – \color{red}{x} + 5y -2\)
\(=3 \color{red}{x^2} + (5y-1) \color{red}{x} – (2y^2 – 5y + 2)\)
(\(\color{red}{x}\) の \(2\) 次式として整理した.)
\(=3 \color{red}{x^2} + (5y-1) \color{red}{x} – (2y-1)(y-2)\)


\(=\{3 \color{red}{x} – (y-2)\}\{\color{red}{x} + (2y-1)\}\)
\(=(3x-y+2)(x+2y-1)\) \(\cdots\) (答)
\((3)\)
\(\color{red}{a} (b^2 – c^2) + b(c^2 – \color{red}{a^2}) + c(\color{red}{a^2} – b^2)\)
\(=(b^2 – c^2) \color{red}{a} + bc^2 – b \color{red}{a^2} + c \color{red}{a^2} – b^2 c\)
\(=-(b-c) \color{red}{a^2} + (b^2 – c^2) \color{red}{a} – b^2 c + bc^2\)
(\(\color{red}{a}\) の \(2\) 次式として整理した.)
\(=- \color{blue}{(b-c)} \color{red}{a^2} + (b+c) \color{blue}{(b-c)} \color{red}{a} – bc \color{blue}{(b-c)}\)
\(=- \color{blue}{(b-c)} \{\color{red}{a^2} – (b+c) \color{red}{a} + bc\}\)
(共通因数 \(- \color{blue}{(b-c)}\) をくくり出した.)
\(=- \color{blue}{(b-c)} (\color{red}{a} – b)(\color{red}{a} – c)\)
\(=-(b-c)(a-b)\{-(c-a)\}\)
\(=(a-b)(b-c)(c-a)\) \(\cdots\) (答)
■ 練習 ■ <複雑な式の因数分解>
次の式を因数分解せよ.
\((1)\) \(x^2 – xy + zx – wx + wy – wz\)
\((2)\) \(2x^2 + 3xy – 2y^2 – 3x – y +1\)
\((3)\) \((a+b+c)(ab+bc+ca)-abc\)
\((1)\) 札幌大 (法・経営・文化)
\((2)\) 中央大 (経)
\((3)\) 札幌学院大
SPONSORED LINK
■ 解答 ■
\((1)\)
\(x^2 – xy + zx – \color{red}{w} x + \color{red}{w} y – \color{red}{w} z\)
\(=(-x+y-z) \color{red}{w} + x^2 -xy + zx\)
(\(\color{red}{w}\) の \(1\) 次式として整理した.)
\(=- \color{blue}{(x-y+z)} \color{red}{w} + x \color{blue}{(x-y+z)}\)
\(=\color{blue}{(x-y+z)}(- \color{red}{w}+x)\)
(共通因数 \(\color{blue}{x-y+z}\) をくくり出した.)
\(=(x-w)(x-y+z)\) \(\cdots\) (答)
\((2)\)
\(2 \color{red}{x^2} + 3 \color{red}{x} y – 2y^2 – 3 \color{red}{x} – y +1\)
\(=2 \color{red}{x^2} + (3y-3) \color{red}{x} – (2y^2 + y -1)\)
(\(\color{red}{x}\) の \(2\) 次式として整理した.)
\(=2 \color{red}{x^2} + (3y-3) \color{red}{x} – (2y-1)(y+1)\)
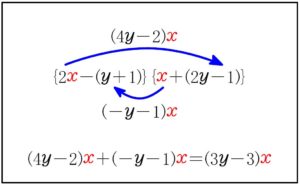

\(=\{2 \color{red}{x} – (y+1)\}\{\color{red}{x} + (2y-1)\}\)
\(=(2x-y-1)(x+2y-1)\) \(\cdots\) (答)
\((3)\)
\((\color{red}{a} +b+c)(\color{red}{a} b+bc+c \color{red}{a}) – \color{red}{a} bc\)
\(=\{\color{red}{a} + (b+c)\} \{(b+c) \color{red}{a} + bc\} – bc \color{red}{a}\)