3項の和の平方 \((a+b+c)^2\) の展開公式を解説します.
● 掛け算の記号に物申す ●
\(1+2\times3\)
という計算を間違える子どもは意外に多くて,
\(2\times3\) の部分を先に計算すべきところを, \(1+2\) を先にしてしまうらしい….
原因の \(1\) つとして, 記号が悪いんじゃないか.
\(1+2\times3\)
では, 記号 「\(+\)」 と 「\(\times\)」 で区切られる数字 \(1\), \(2\), \(3\) は 「等間隔」 に並んでいて,
\(1\) と \(2\) の結びつきよりも \(\color{red}{2}\) と \(\color{red}{3}\) の結びつきのほうが強い のに, そのようには見えないよね.
だから先に \(1+2\) をやりにいってしまう子が出てくる.
そこで, 「\(\times\)」 を 「\(\cdot\)」 に代えて
\(1+\color{red}{2\cdot 3}\)
と書けば \(\color{red}{2}\) と \(\color{red}{3}\) の間隔が詰まって見え,
「そこを先に計算!」 という意識がはたらき,
計算ミスが減るんじゃないか.
これからは, 記号 「\(\color{red}{\cdot}\)」 は掛け算を表す記号として用いる.
● 整式って? ●
いくつかの用語を説明しておこう.
数や文字およびそれらを掛け合わせてできる式が \(\large\bf\color{blue}{単項式}\) (\(\rm{monomial}\)) だ.
ただし, 掛け算の記号 「\(\times\)」, 「\(\cdot\)」 は省略してかく.
例
\((1)\) \(5\)
\((2)\) \(x\) (\(=1 \cdot x\))
\((3)\) \(-2a^2\) (\(=(-2) \cdot a \cdot a\))
\((4)\) \(3 x^2 y\) (\(=3 \cdot x \cdot x \cdot y\))
単項式において,
文字に掛けられた数の部分をその単項式の \(\large\bf\color{blue}{係数}\) (\(\rm{coefficient}\)),
掛け合わせた文字の個数をその単項式の \(\large\bf\color{blue}{次数}\) (\(\rm{degree}\))
という.
「次数は字数」 と覚えよう.
例
\((1)\) \(\color{teal}{5}\)
\(\cdots\) 係数 \(\color{teal}{5}\), 次数 \(\color{magenta}{0}\)
(単項式 \(0\) については, その次数は考えない.)
\((2)\) \(\color{teal}{-2} \color{magenta}{x}\) (\(=\color{teal}{(-2)} \cdot \color{magenta}{x}\))
\(\cdots\) 係数 \(\color{teal}{-2}\), 次数 \(\color{magenta}{1}\)
\((3)\) \(\color{magenta}{a^2}\) (\(=\color{teal}{1} \cdot \color{magenta}{a} \cdot \color{magenta}{a}\))
\(\cdots\) 係数 \(\color{teal}{1}\), 次数 \(\color{magenta}{2}\)
\((4)\) \(\color{teal}{7} \color{magenta}{x^2 y}\) (\(=\color{teal}{7} \cdot \color{magenta}{x} \cdot \color{magenta}{x} \cdot \color{magenta}{y}\))
\(\cdots\) 係数 \(\color{teal}{7}\), 次数 \(\color{magenta}{3}\)
次が重要!
単項式に複数の文字が含まれているとき,
特定の文字に着目して 係数と次数を考えることがあるぞ.
例えば \(7 x^2 y\) は,
\(\color{red}{x}\) に着目 \(7y \color{red}{x^2}\)
\(\cdots\) 係数 \(7y\), 次数 \(\color{red}{2}\)
\(\color{red}{y}\) に着目 \(7x^2 \color{red}{y}\)
\(\cdots\) 係数 \(7x^2\), 次数 \(\color{red}{1}\)
といった具合だ.
そして,
\(x^3 + 5xy + 2xy + (-3 y^2)\)
のように,
いくつかの単項式の和で表される式を \(\large\bf\color{blue}{多項式}\) (\(\rm{polynomial}\)),
各単項式をその多項式の \(\large\bf\color{blue}{項}\) (\(\rm{term}\))
という.
さらに, 単項式と多項式を合わせて \(\large\bf\color{blue}{整式}\) (\(\rm{integral\ expression}\)) とよぶんだ.
また, 整式
\(x^3 + 5xy + 2xy + (-3 y^2)\)
における \(5\color{red}{xy}\) と \(2\color{red}{xy}\) のように,
文字の部分が同じである項を \(\large\bf\color{blue}{同類項}\) (\(\rm{similar\ term}\)) という.
これらは係数をまとめて
\((5+2)xy=7xy\)
と表されるね.
そして, \(+(-3y^2)\) は単に \(-3y^2\) とかくので, 整式
\(x^3 + 5xy + 2xy + (-3 y^2)\)
を \(\large\bf\color{blue}{整理}\) すると
\(x^3 + 7xy – 3y^2\)
となるわけだ.
同類項をまとめて整理した整式において,
最高次数の項の次数を この整式の \(\large\bf\color{blue}{次数}\) といい,
次数が \(n\) である整式を \(\large\color{blue}{n}\) \(\large\bf\color{blue}{次式}\) という.
整式
\(x^3 + 7xy – 3y^2\)
は, \(3\) 次の項 \(x^3\) が最も次数の高い項なので \(3\) 次式ということになるね.
特定の文字にも着目してみよう.
\(\color{red}{x}\) に着目すると
\(\color{red}{x^3} + 7y \color{red}{x} – 3y^2\)
は \(\color{red}{x}\) の \(\color{red}{3}\) 次式 で,
\(\color{red}{x}\) を含まない項 (\(0\) 次の項) を \(\large\bf\color{blue}{定数項}\) (\(\rm{constant\ term}\)) という.
また, \(\color{red}{y}\) に着目すると
\(x^3 + 7x \color{red}{y} – 3 \color{red}{y^2}\)
は \(\color{red}{y}\) の \(\color{red}{2}\) 次式 で,
定数項は \(\color{red}{y}\) を含まない \(x^3\) だね.
● 分配法則で括弧をはずす ●
縦の長さが \(a\), 横の長さが \(b+c\) である長方形の面積は
縦 \(\times\) 横 で
\(a(b+c)\)
これは縦 \(a\) 横 \(b\) の長方形と, 縦 \(a\) 横 \(c\) の長方形に分割してそれらを加え合わせたものに等しいよね.
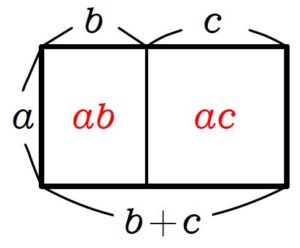
つまり,
\(\large\color{blue}{a(b+c)=ab+ac}\)
\((\ \ \ \ \ )\) の前の \(a\) を, 中の \(b\) と \(c\) に分配して掛けているので,
\(\large\bf\color{blue}{分配法則}\) (\(\rm{distributive\ law}\)) という.
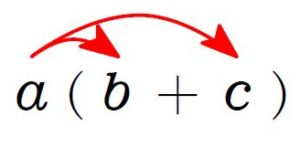
いわゆる 「括弧をはずす」 という計算だ.
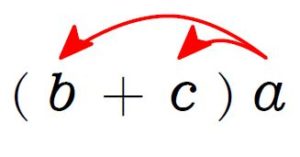
掛け算は順序を入れ替えても同じなので, \(a\) を \((\ \ \ \ \ )\) の後ろから掛けても同じね.
分配法則を使えばこんな式の括弧もはずせる.
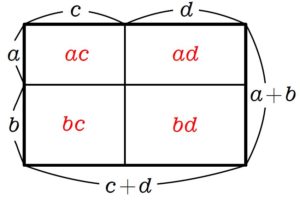
\((a+b)(c+d)\)
\(=(a+b)M\)
(\(c+d=M\) とおいた.)
\(=aM+bM\)
\(=a(c+d)+b(c+d)\)
\(=ac+ad+bc+bd\)
すなわち,
\(\large\color{blue}{(a+b)(c+d)}\) \(\large\color{blue}{=ac+ad+bc+bd}\)
結果的には前の \((\ \ \ \ \ )\) 内の \(a\), \(b\) をそれぞれ後ろの \(c\), \(d\) に分配して掛けたようになっている.
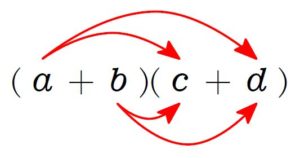
縦 \(a+b\), 横 \(c+d\) の長方形の面積を考えても納得できるね.
● 乗法公式で展開する ●
整式どうしを掛け算し, \(1\) つの整式で表すのが \(\large\bf\color{blue}{展開}\) (\(\rm{expansion}\)) だ.
そして, 掛け算のことを \(\large\bf\color{blue}{乗法}\) (\(\rm{multiplication}\)) ともいい,
整式の乗法を公式化したものが お茶の間で有名な次の \(\large\bf\color{blue}{乗法公式}\) だ.
分配法則を用いて導かれるぞ.
\([1]\) \(\large\color{blue}{(x+a)(x+b)}\) \(\large\color{blue}{=x^2+(a+b)x+ab}\)
\([2]\) \(\large\color{blue}{(a+b)^2=a^2+2ab+b^2}\)
\([3]\) \(\large\color{blue}{(a-b)^2=a^2-2ab+b^2}\)
\([4]\) \(\large\color{blue}{(a+b)(a-b)=a^2-b^2}\)
左辺から右辺へと見ると展開公式,
右辺から左辺へと見ると因数分解公式になる.
さて, \([2]\) の式についてだが, 一般に \((a+b)^2\) が \(a^2+b^2\) に 等しくない のはなぜ?
これは \(1\) 辺が \(a+b\) \((a>0\), \(b>0)\) の正方形の面積を考えるとよくわかる.
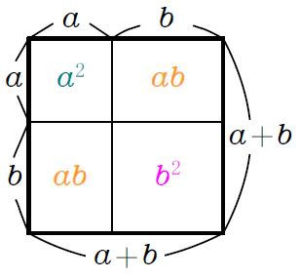
全体の面積 \((a+b)^2\) は
\(\color{teal}{a^2}+\color{orange}{ab}+\color{orange}{ab}+\color{magenta}{b^2}\)
つまり
\(\color{teal}{a^2}+2\color{orange}{ab}+\color{magenta}{b^2}\)
であって, \(a^2+b^2\) とはならないよね.
<補足> \([1]\) ~ \([4]\) を分配法則を用いて導くと次のようになります.
\([1]\)
\((x+a)(x+b)\)
\(=x^2 + xb + ax + ab\)
\(=x^2 + (a+b)x + ab\)
\([2]\)
\((a+b)^2\)
\(=(a+b)(a+b)\)
\(=a^2 + ab + ba + b^2\)
\(=a^2 + 2ab + b^2\)
\([3]\)
\((a-b)^2\)
\(=(a-b)(a-b)\)
\(=a^2 – ab – ba + b^2\)
\(=a^2 -2ab + b^2\)
\([4]\)
\((a+b)(a-b)\)
\(=a^2 – ab + ba – b^2\)
\(=a^2 – b^2\)
● 3項の和の平方 ●
では, \(3\) 項の和の平方 \((a+b+c)^2\) を展開するとどんな式になるかな?
同じく正方形の面積で考えてみよう.
\(1\) 辺が \(a+b+c\) の正方形の面積は, \((a+b+c)^2\) である一方…
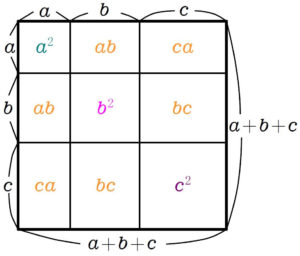
それは縦横の線で分割された \(9\) つのエリアの面積の和
\(\color{teal}{a^2}+\color{magenta}{b^2}+\color{purple}{c^2}\) \(+\color{orange}{ab}+\color{orange}{ab}+\color{orange}{bc}+\color{orange}{bc}+\color{orange}{ca}+\color{orange}{ca}\)
\(=\color{teal}{a^2}+\color{magenta}{b^2}+\color{purple}{c^2}+2\color{orange}{ab}+2\color{orange}{bc}+2\color{orange}{ca}\)
に等しい. すなわち,
\(\large\color{blue}{(a+b+c)^2}\) \(\large\color{blue}{=a^2+b^2+c^2+2ab+2bc+2ca}\) \(\cdots\) ①
が成り立つ.
覚える前に, 理解する!
これが大事.
上のように理解しておけば, ちょっとひねられても, 例えば \((a+b+c+d)^2\) の展開式をかけと言われても同じようにできるでしょう.
「そんな公式, 習っていません.」
というのは, 理解と思考を放棄した者のセリフなのだ.
<補足> \([2]\) の式を直接利用して導くと次のようになります.
\(\ \ \ (a+b+c)^2\)
\(\ \ \ \ =\{(a+b)+c\}^2\)
\(\ \ \ \ =(A+c)^2\) \((A=a+b)\)
\(\ \ \ \ =A^2+2Ac+c^2\)
\(\ \ \ \ =(a+b)^2+2(a+b)c+c^2\)
\(\ \ \ \ =a^2+2ab+b^2+2ac+2bc+c^2\)
\(\ \ \ \ =a^2+b^2+c^2+2ab+2bc+2ca\)
● A, B, C は何でもいい ●
① の式は, 文字を替えて,
\(\large\color{blue}{(A+B+C)^2}\) \(\large\color{blue}{=A^2+B^2+C^2}\) \(\large\color{blue}{+2AB+2BC+2CA}\)
としても, その式のもつ意味は変わらない.
そして, \(\color{blue}{A}\), \(\color{blue}{B}\), \(\color{blue}{C}\) にあたるものは, 数を表すものなら何でもいい. 食べ物や乗り物でなければね.
例えば, \(\color{blue}{A}=\color{teal}{a}\), \(\color{blue}{B}=\color{magenta}{2b}\), \(\color{blue}{C}=\color{orange}{-3c}\) なら こうなる.
\(\{\color{teal}{a}+\color{magenta}{2b}+(\color{orange}{-3c})\}^2\)
\(=\color{teal}{a}^2+(\color{magenta}{2b})^2+(\color{orange}{-3c})^2\) \(+2\cdot \color{teal}{a}\cdot \color{magenta}{2b} + 2\cdot \color{magenta}{2b} \cdot (\color{orange}{-3c}) + 2\cdot (\color{orange}{-3c})\cdot \color{teal}{a}\)
Point <展開 (3項の和の平方)> ★★
\(\large\color{blue}{(a+b+c)^2}\) \(\large\color{blue}{=a^2+b^2+c^2+2ab+2bc+2ca}\)
\(a\), \(b\), \(c\) にあたるものは, 数を表すものなら何でもよい.
■ 例題 ■ <展開 (3項の和の平方)>
\((a+2b-3c)^2\) を展開せよ.
亀田医療大 (看)
SPONSORED LINK
■ 解答 ■
\((a+2b-3c)^2\)
\(=\{\color{teal}{a}+\color{magenta}{2b}+(\color{orange}{-3c})\}^2\)
\(=\color{teal}{a}^2+(\color{magenta}{2b})^2+(\color{orange}{-3c})^2\) \(+2\cdot \color{teal}{a}\cdot \color{magenta}{2b} + 2\cdot \color{magenta}{2b} \cdot (\color{orange}{-3c}) + 2\cdot (\color{orange}{-3c})\cdot \color{teal}{a}\)
\(=a^2+4b^2+9c^2+4ab-12bc-6ca\) \(\cdots\) (答)
次の練習問題は自力で解いてみましょう.
■ 練習 ■ <展開 (3項の和の平方)>
次の式を展開せよ.
\((1)\) \((-x+2y-4)^2\)
\((2)\) \((x^2-2\sqrt{3}x+y^2)^2\)
\((1)\) 城西国際大 (看)
\((2)\) 香川大 (医)
SPONSORED LINK
■ 解答 ■
\((1)\)
\(\large\color{blue}{(A+B+C)^2}\) \(\large\color{blue}{=A^2+B^2+C^2}\) \(\large\color{blue}{+2AB+2BC+2CA}\)
で \(\color{blue}{A}=\color{teal}{-x}\), \(\color{blue}{B}=\color{magenta}{2y}\), \(\color{blue}{C}=\color{orange}{-4}\) とする.
\((-x+2y-4)^2\)
\(=\{(\color{teal}{-x})+\color{magenta}{2y}+(\color{orange}{-4})\}^2\)
\(=(\color{teal}{-x})^2+(\color{magenta}{2y})^2+(\color{orange}{-4})^2\) \(+2\cdot (\color{teal}{-x})\cdot \color{magenta}{2y}\) \(+2\cdot \color{magenta}{2y}\cdot (\color{orange}{-4})\) \(+2\cdot (\color{orange}{-4})\cdot (\color{teal}{-x})\)
\(=x^2+4y^2+16-4xy-16y+8x\)
\(=x^2-4xy+4y^2+8x-16y+16\) \(\cdots\) (答)
\((2)\)
\(\large\color{blue}{(A+B+C)^2}\) \(\large\color{blue}{=A^2+B^2+C^2}\) \(\large\color{blue}{+2AB+2BC+2CA}\)
で \(\color{blue}{A}=\color{teal}{x^2}\), \(\color{blue}{B}=\color{magenta}{-2\sqrt{3}x}\), \(\color{blue}{C}=\color{orange}{y^2}\) とする.
\((x^2-2\sqrt{3}x+y^2)^2\)
\(=\{\color{teal}{x^2}+(\color{magenta}{-2\sqrt{3}x})+\color{orange}{y^2}\}^2\)
\(=(\color{teal}{x^2})^2+(\color{magenta}{-2\sqrt{3}x})^2+(\color{orange}{y^2})^2\) \(+2\cdot \color{teal}{x^2}\cdot(\color{magenta}{-2\sqrt{3}x})\) \(+2\cdot (\color{magenta}{-2\sqrt{3}x})\cdot \color{orange}{y^2}\) \(+2\cdot \color{orange}{y^2}\cdot \color{teal}{x^2}\)
\(=x^4+12x^2+y^4\) \(4\sqrt{3}x^3-4\sqrt{3}xy^2+2x^2 y^2\)
\(=x^4+2x^2 y^2+y^4\) \(-4\sqrt{3}x^3-4\sqrt{3}xy^2+12x^2\) \(\cdots\) (答)
\((x-a)(x-b)(x-c)\cdots (x-z)\)
の計算結果はなんと \(0\). (最後から \(3\) 番目の ( ) に注目.)
これはまさに意外な 「展開」.